Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Hàm số bậc nhất
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 101:
Với mỗi số thực a, ta gọi phần nguyên của số a là số nguyên lớn nhất không vượt quá a và kí hiệu là [a]. Chứng minh rằng với mọi n nguyên dương ta luôn có:
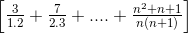= n
Bài 102:
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = (k - 1)x + n và hai điểm
A(0; 2), B(-1; 0).
Câu hỏi số 1:
Tìm các giá trị của k và n để đường thẳng (d) đi qua hai điểm A và B.
Câu hỏi số 2:
Tìm các giá trị của k và n để đường thẳng (d) song song với đường thẳng ( ∆): y = x + 2 -k.
Câu hỏi số 3:
Cho n = 2. Tìm k để đường thẳng (d) cắt trục Ox tại C sao cho diện tích tam giác OAC gấp hai lần diện tích tam giác OAB.
Câu hỏi số 103:
Cho hàm số y = 2x + 2m + 1. Xác định m, biết rằng đồ thị hàm số đi qua điểm A(1; 4)
Câu hỏi số 104:
Cho hàm số bậc nhất y = ax + 1. Xác định hệ số a, biết rằng đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 
Câu hỏi số 105:
Cho hàm số: y = -2x có đồ thị là (d)
hàm số : y = x - 1 có đồ thị là (d')
Xác định các hệ số a,b biết đường thẳng (D): y = ax + b song song với (d) và cắt(d') tại điểm có tung độ bằng -3.
Bài 106:
Cho hàm số y = mx - 2m + 1 có đồ thị (d) và điểm A(2;1)
Câu hỏi số 1:
Viết phương trình đường thẳng OA
Câu hỏi số 2:
Tìm m để khoảng cách từ O đến d lớn nhất.
Câu hỏi số 107:
Trên cùng một mặt phẳng tọa độ, cho hai đường thẳng:
(d): y = -x và (d'): y = x + 2
Viết phương trình đường thẳng (D) song song với (d) và cắt (d') tại điểm có hoành độ bằng 1.
Câu hỏi số 108:
Cho (D1): y = 2x và (D2) : y = -x + 3
Tìm tọa độ giao điểm A của (D1) và (D2) bằng phép tính.
Câu hỏi số 109:
Cho hình bình hành ABCD và n = 4k + 1 ( k nguyên dương) đường thẳng. Mỗi đường thẳng đó chia hình bình hành ABCD thành 2 hình thang có tỉ số diện tích là m ( m là số nguyên dương cho trước). Chứng minh rằng có ít nhất k + 1 đường thẳng trong số n đường thẳng nói trên đồng quy. ( Hình bình hành cũng được xem như hình thang).
Câu hỏi số 110:
Cho a,b,c là ba số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
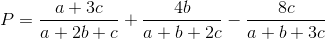
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
