Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Hàm số bậc nhất
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 111:
Hai người chơi trò chơi như sau: Trong hộp có 311 viên bi, lần lượt từng người lấy k viên bi, với K ϵ {1;2;3}. Người chiến thắng là người lấy được viên bi cuối cùng trong hộp đó.
Câu hỏi số 1:
Hỏi người thứ nhất hay người thứ hai chiến thắng và chiến thuật chơi như thế nào để chiến thắng?
Câu hỏi số 2:
Cũng hỏi như câu trên khi đề bài thay 311 viên bi bằng n viên bi, với n là số nguyên dương?
Câu hỏi số 112:
Phân tích đa thức 4(1 + x)(1 + y)(1 + x + y) – 3x2y2 thành nhân tử
Câu hỏi số 113:
Cho các số thực x,y thay đổi và thỏa mãn 4x2 - ( 8y + 11)x + (8y2 + 14)=0
Tìm y khi x lần lượt đạt được giá trị lớn nhất, nhỏ nhất
Câu hỏi số 114:
Tìm các cặp số nguyên dương thỏa mãn:
6x+5y+18=2xy
Câu hỏi số 115:
Cho các số a,b ,c thỏa mãn các điều kiện 0 < a < b và phương trình ax2 + bx + c = 0 vô nghiệm. Chứng minh rằng :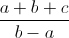 
> 3
Câu hỏi số 116:
Rút gọn biểu thức P =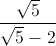 
- 2√5.
Bài 117:
Cho a, b , c là các số nguyên sao cho 2a + b, 2b + c, 2c + a đều là các số chính phương (*).
Câu hỏi số 1:
Biết rằng có ít nhất một trong ba số chính phương nói trên chia hết cho 3. Chứng minh rằng tích (a – b)(b – c)(c – a) chia hết cho 27.
Câu hỏi số 2:
Tồn tại hay không các số nguyên a, b, c thỏa mãn điều kiện (*) sao cho (a – b)(b – c)(c – a) không chia hết cho 27.
Câu hỏi số 118:
Cho a, b là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức P =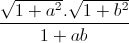 
Câu hỏi số 119:
Cho x, y là các số thực dương thỏa mãn điều kiện xy ≤ 1. Chứng minh rằng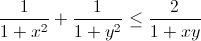 
. Dấu bằng xảy ra khi và chỉ khi nào?
Câu hỏi số 120:
Cho a, b, c là ba số nguyên thỏa mãn a + b + c = 0. Chứng minh rằng a5 + b5 + c5 chia hết cho 5.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
