Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Hệ thức lượng trong tam giác vuông
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 51:
Cho hình thang cân ABCD (AB // CD, AB < CD). M và N là trung điểm của hai đường chéo BD và AC
a. Chứng minh các tứ giác AMNB và DMNC là những hình thang cân.
b. Chứng minh BM2 = AM2 + MN.AB
Câu hỏi số 52:
Cho hình thang ABCD (AB // CD) có hai đường chéo vuông góc với nhau (AC ⊥ BD)
a. Chứng minh tổng các bình phương của hai đáy bằng tổng các bình phương của hai cạnh bên (AB2 + BD2 = AD2 + BC2).
b. Chứng minh tổng các bình phương của hai đường chéo bằng bình phương của tổng hai đáy [AC2 + BD2 = (AB + CD)2].
c. Kẻ đường cao AH và đường trung bình Mn của hình thang ABCD. Biết BD = 9 cm, AC = 12 cm. Tính diện tích tứ giác AMHN.
Câu hỏi số 53:
Cho hình chữ nhật ABCD, kẻ DE ⊥ AC. Gọi M và N theo thứ tự là trung điểm cảu BC và AE.
a. Chứng minh EA : EC =(BC : AB)2.
b. Chứng minh MN2 + ND2 = MC2 + CD2.
Câu hỏi số 54:
Cho tam giác ABC, đường cao AH. Chứng minh rằng:
a. Nếu AB2 = BH.BC thì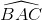 
= 900.
b. Nếu HA2 = BH.HC thì 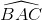= 900.
c. Nếu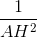 
= 
+ 
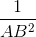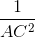và AH.BC = AB.AC thì 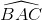= 900
Câu hỏi số 55:
Cho tam giác cân ABC (AB = AC). Tia phân giác Ax của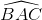 
cắt BC tại H. Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho BM = CN
a. Nối MN cắt BC tại I, chứng minh I là trung điểm của MN
b. Trung trực của MN cắt Ax tại O, chứng minh OC ⊥ AC.
c. Chứng minh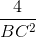 
= 
+ 
.
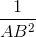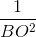d. Biết AB = 6 cm, OB = 4,5 cm, tính diện tích ∆ABC.
Câu hỏi số 56:
Cho tam giác vuông cân ABC (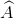
= 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
a. Chứng minh tứ giác ABEC là hình vuông.
b. Chứng minh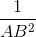 
= 
+ 
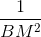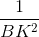
c. Biết BM = 6 cm. Tính các cạnh của tam giác MCK.
Câu hỏi số 57:
Cho tam giác ABC có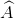 
= 60°. Chứng minh rằng BC2 = AB2 + AC2 - AB.AC.
Câu hỏi số 58:
Cho tam giác ABC có BC = 9cm,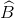 
= 60°, 
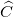= 40°. Kẻ đường cao АН của tam giác đó. Hãy tính AH, AB, AC (làm tròn kết quả đến chữ số thập phân thứ nhất).
Bài 59:
Hãy tính góc nhọn tạo bởi tia nắng mặt trời với mặt đất (làm tròn kết quả đến độ) trong các trường hợp sau :
Câu hỏi số 1:
Độ dài của bóng gấp đôi chiều cao của người.
Câu hỏi số 2:
Độ dài của bóng bằng nửa chiều cao của người
Câu hỏi số 60:
Không dùng bảng và máy tính bỏ túi, hãy sắp xếp giá trị các tỉ số lượng giác sau đây theo thứ tự lớn đến nhỏ : tg 70°, cotg 60°, cotg 65°, tg 50°, sin 25°.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
