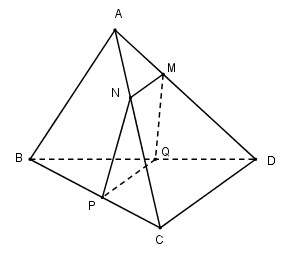
Cho tứ diện đều ABCD cạnh a. Gọi M và P lần lươt là hai điểm di động trên các cạnh AD và BC
Cho tứ diện đều ABCD cạnh a. Gọi M và P lần lươt là hai điểm di động trên các cạnh AD và BC sao cho MA = PC = x (0 < x < a). Mặt phẳng \(\left( \alpha \right)\) đi qua MP song song với CD cắt tứ diện theo một thiết diện là hình gì?
Đáp án đúng là: D
Quảng cáo
- Đưa về cùng mặt phẳng.
- Sử dụng các tính chất về đường cao, đường trung tuyến trong tam giác cân.
- Vận dụng các dấu hiệu nhận biết một số tứ giác đặc biệt.
Ta có: \(\left\{ \matrix{ M \in \left( \alpha \right) \cap \left( {ACD} \right) \hfill \cr CD\parallel \left( \alpha \right) \hfill \cr CD \subset \left( {ACD} \right) \hfill \cr} \right.\)
Suy ra \(\left( \alpha \right) \cap \left( {ACD} \right) = MN\parallel CD\) với \(N \in AC\).
Tương tự \(\left( \alpha \right) \cap \left( {BCD} \right) = PQ\parallel CD\) với \(Q \in BD.\)
Vì MN // CD // PQ nên thiết diện MNPQ là hình thang.
Ta có DQ = CP = x, DM = a – x.
Áp dụng định lí Cosin trong tam giác DMQ ta có:
\(MQ = \sqrt {D{M^2} + D{Q^2} - 2DM.DQ.cos60} = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Tương tự ta cũng tính được \(NP = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Suy ra MQ = NP.
Vậy thiết diện MNPQ là hình thang cân.
Chọn D.
Học sinh chưa biết áp dụng định lí Côsin trong tam giác hoặc áp dụng nhưng bị sai dấu. Công thức đúng là \({a^2} = {b^2} + {c^2} - 2bc\cos A.\)
Tuy nhiên rất nhiều học sinh bị nhầm dấu “ – “ thành dấu “ + “, tức là: \({a^2} = {b^2} + {c^2} + 2bc\cos A.\) Hoàn toàn sai nhé!
Đáp án cần chọn là: D
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
