Hai chiếc thuyền đang ở cùng một vĩ tuyến, cách nhau một khoảng \(9\) hải lý. Vào lúc \(6h\)
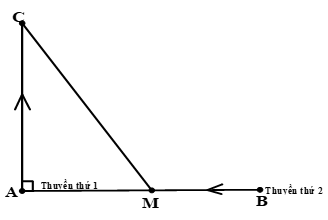
Hai chiếc thuyền đang ở cùng một vĩ tuyến, cách nhau một khoảng \(9\) hải lý. Vào lúc \(6h\) cả hai cùng xuất phát, chiếc thuyền thứ nhất đi theo hướng Bắc với vận tốc \(6\) hải lý/ giờ. Chiếc thuyền thứ hai đi theo hướng về vị trí ban đầu của chiếc thuyền thứ nhất với vận tốc \(4\) hải lý/ giờ. Hỏi đến \(6h45\) phút thì khoảng cách giữa hai chiếc thuyền là bao nhiêu km? Biết \(1\) hải lý \( = 1852m\)
Đáp án đúng là: B
Quảng cáo
Điểm mấu chốt của bài toán nằm ở việc hiểu được “hai thuyền ở cùng một vĩ tuyến” là như thế nào?
Các em lưu ý, trong môn Địa Lý vĩ tuyến là các đường nằm theo chiều ngang của Trái Đất.
(cụ thể có 5 đường vĩ tuyến, trong đó, có một đường vĩ tuyến mà em nào cũng biết đó là đường xích đạo- các em tìm hiểu kỹ trong môn Địa Lý nhé!)
Sau khi đã biết về đường vĩ tuyến và phương hướng trên Trái Đất các em phải vẽ lại hình cho bài toán để dựa vào đó giải ra đáp số.
Vẽ lại sơ đồ bài toán như hình vẽ:
Vì lúc đầu hai chiếc thuyền ở cùng một vĩ tuyến ta biễu diễn theo phương ngang \(AB\)
Sau khi xuất phát, thuyền thứ hai đi về hướng Bắc nên ta biểu diễn theo hướng \(AC\) hướng thẳng lên
Thuyền thứ hai đi trở về vị trí thuyền thứ nhất tức là hướng từ \(B\) sang \(A\)
Hướng Nam-Bắc vuông góc với vĩ tuyến nên \(AB\) vuông góc với \(AC\) tại \(A\) .
\(AB = 9\) hải lý là khoảng cách lúc đầu giữa hai thuyền.
\(AC\) là quãng đường thuyền thứ nhất đi được, \(BM\) là quãng đường thuyền thứ hai đi được trong cùng một khoảng thời gian.
\(CM\) là khoảng cách giữa hai thuyền lúc sau.
Thời gian đi của hai thuyền
t = 6h45phút – 6h = 45phút = \(\dfrac{3}{4}h\)
Quãng đường mà thuyền thứ nhất đi được:
\(AC = {v_1}.{\text{ }}t = 6.\dfrac{3}{4} = 4,5\) ( hải lý)
Quãng đường mà thuyền thứ hai đi được:
\(BM = {v_1}.{\text{ }}t = 4.\dfrac{3}{4} = 3\) ( hải lý)
Độ dài đoạn \(AM\) :
\(AM = \;9-3 = 6\) (hải lý)
Xét \(\Delta ABM\)vuông tại \(A\) , áp dụng định lý Pitago, ta có:
\(A{M^2} + A{C^2} = C{M^2} \Leftrightarrow C{M^2} = 4,{5^2} + {6^2} = 56,25 \Leftrightarrow CM = 7,5\) (hải lý)
\(7,5\) (hải lý) \( = 7,5.1,852\) km \( = 13,89\) km (\(1\) hải lý\( = 1852m = 1,852km\))
Vậy: Đến \(6h45\) phút thì khoảng cách giữa hai chiếc thuyền là \(13,89\)km.
Bình luận về bài toán:
Các em lưu ý, không nên đổi vận tốc từ hải lý/ giờ ra km/giờ, mà chúng ta vẫn để đơn vị hải lý/ giờ để tính toán. Được kết quả cuối cùng ta mới đổi từ đơn vị hải lý ra đơn vị km dựa vào phần đổi đơn vị mà đề đã cho.
Đáp án cần chọn là: B
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
