Chọn câu trả lời đúng Xét bài toán: Cho tam giác ABC và \(A'B'C'\) có
Chọn câu trả lời đúng
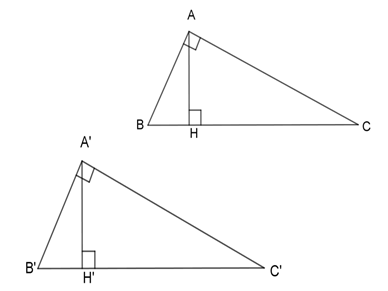
Xét bài toán: Cho tam giác ABC và \(A'B'C'\) có \(\widehat{BAC}=\widehat{B'A'C'}={{90}^{0}}\) và có các đường cao lần lượt là AH, \(A'H'\). Biết rằng \(\frac{AH}{AB}=\frac{A'H'}{A'B'}\). Chứng minh rằng \(\Delta ABC\backsim \Delta A'B'C'\).
Sắp xếp các ý sau một cách hợp lý để có lời giải bài toán trên:
(1) Ta có \(\Delta ABH\backsim \Delta A'B'H'\Rightarrow \widehat{ABH}=\widehat{A'B'H'}\)\(\Rightarrow \widehat{ABC}=\widehat{A'B'C'}\)
(2) Xét \(\Delta ABH\ (\widehat{AHB}={{90}^{0}})\) và \(\Delta A'B'H'\ (\widehat{A'H'B'}={{90}^{0}})\) có:
\(\frac{AH}{A'H'}=\frac{AB}{A'B'}\) (vì \(\frac{AH}{AB}=\frac{A'H'}{A'B'}\ (gt)\))
Do đó \(\Delta ABH\backsim \Delta A'B'H'\) (g – g)
(3) Xét \(\Delta ABC\ (\widehat{BAC}={{90}^{0}})\) và \(\Delta A'B'C'\ (\widehat{B'A'C'}={{90}^{0}})\) có:
\(\widehat{ABC}=\widehat{A'B'C'}\) (cmt)
Do đó \(\Delta ABC\backsim \Delta A'B'C'\) (g – g)
Đáp án đúng là: D
Quảng cáo
- Áp dụng lý thuyết về các trường hợp đồng dạng của tam giác vuông để tìm ra điều phải chứng minh.
Xét \(\Delta ABH\ (\widehat{AHB}={{90}^{0}})\) và \(\Delta A'B'H'\ (\widehat{A'H'B'}={{90}^{0}})\) có:
\(\frac{AH}{A'H'}=\frac{AB}{A'B'}\) (vì \(\frac{AH}{AB}=\frac{A'H'}{A'B'}\ (gt)\))
Do đó \(\Delta ABH\backsim \Delta A'B'H'\) (g – g)
Ta có \(\Delta ABH\backsim \Delta A'B'H'\Rightarrow \widehat{ABH}=\widehat{A'B'H'}\)\(\Rightarrow \widehat{ABC}=\widehat{A'B'C'}\)
Xét \(\Delta ABC\ (\widehat{BAC}={{90}^{0}})\) và \(\Delta A'B'C'\ (\widehat{B'A'C'}={{90}^{0}})\) có:
\(\widehat{ABC}=\widehat{A'B'C'}\) (cmt)
Do đó \(\Delta ABC\backsim \Delta A'B'C'\) (g – g)
Đáp án cần chọn là: D
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
