Dynamo là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynamo làm ma

Câu hỏi số 230382:

Thông hiểu

Dynamo là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynamo làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diến nào của anh chảng trẻ tuổi tài cao này đều khiến người xem há hốc miệng kinh ngạc vì nó vượt qua giới hạn của khoa học. Một lần đến New York anh ngấu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di truyển từ tòa nhà này đến toà nhà khác và trong quá trình anh di chuyển đấy có một lần anh đáp đất tại một điểm trong khoảng cách của hai tòa nhà ( Biết mọi di chuyển của anh đều là đường thẳng ). Biết tòa nhà ban đầu Dynamo đứng có chiều cao là a(m), tòa nhà sau đó Dynamo đến có chiều cao là b(m)(a < b) và khoảng cách giữa hai tòa nhà là c(m). Vị trí đáp đất cách tòa nhà thứ nhất một đoạn là x(m) hỏi x bằng bao nhiêu để quãng đường di chuyển của Dynamo là bé nhất.

A. \(x=\frac{3ac}{a+b}\)

B. \(x=\frac{ac}{3(a+b)}\)

C. \(x=\frac{ac}{a+b}\)

D. \(x=\frac{ac}{2(a+b)}\)

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:230382

Phương pháp giải

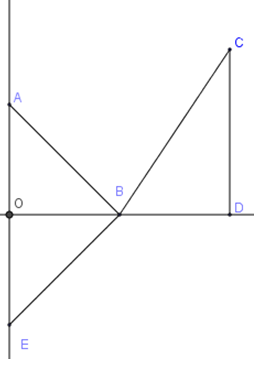
Trong một số bài tập tìm điều kiện của ẩn để biểu thức đạt giá trị lớn nhất hoặc nhỏ nhất ta có thể dùng phương pháp tọa độ để giải

+ Gắn hệ trục tọa độ phù hợp

+ Xác định tọa độ các điểm cần thiết

+ Chuyển yêu cầu bài toán thành yêu cầu liên quan đến các yếu tố trong mặt phẳng.

Giải chi tiết

Gắn hệ trục tọa độ Oxy như hình vẽ, có OA=a; OB=x; OD=c; CD=b

Lấy E là điểm đối xứng với A qua OD.

Ta có E(0;-a); B(x;0); C(c;b)

Yêu cầu bài toán là tìm x để AB+BC nhỏ nhất

Mà ta có AB=EB nên suy ra AB+BC=EB+BC

Khi đó EB+BC nhỏ nhất khi và chỉ khi E,B,C thẳng hàng.

Có \(\overrightarrow{EB}\left( x;a \right);\overrightarrow{CE}\left( c;b+a \right)\) E,B,C thẳng hàng khi và chỉ khi \(\overrightarrow{EB}\) và \(\overrightarrow{CE}\) cùng phương hay \(\frac{x}{c}=\frac{a}{b+a}\Rightarrow x=\frac{ac}{a+b}\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.