1. Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia
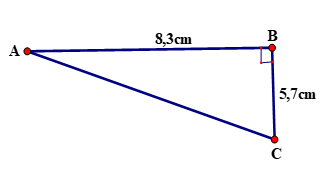
1. Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (hình vẽ)
1a) Hỏi góc tạo bởi chùm tia với mặt da?
1b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?
2. Trước nhà thầy Tưởng có một cây cột điện cao 9m bị cơn bão Tembin vừa qua làm gãy ngang thân, ngọn cây cột điện chạm đất cách gốc 3m. Hỏi điểm gãy ngang của cây cột điện cách gốc bao nhiêu?
Đáp án đúng là: C
Quảng cáo
1.1a)
Đặt tên vị trí các điểm A, B, C như trong hình vẽ, trong đó:
AB = 8,3cm, BC = 5,7cm .
Đường đi của chùm tia tới khối u tương ứng với độ dài của đoạn AC trên hình, góc tạo bởi chùm tia với mặt da là góc BAC.
Xét tam giác vuông ABC, ta có:
\(\tan BAC=\frac{BC}{AB}=\frac{5,7}{8,3}\Rightarrow \angle BAC\approx 34,{{5}^{0}}\)
Vậy góc tạo bởi chùm tia với mặt da gần bằng 34,50
1.1b)
· Áp dụng định lý Pitago cho tam giác vuông ABC, ta có:
\(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{8,{{3}^{2}}+5,{{7}^{2}}}=\sqrt{101,38}\approx 10,1cm\)
Vậy Chùm tia phải đi một đoạn dài gần bằng 10,1cm để đến được khối u.
2. Vẽ lại hình minh họa và đặt tên các vị trí tương ứng như trong hình vẽ. Trong đó, AC’ = m là chiều cao cây cột điện, AC = 3m là khoảng từ ngọn cây cột điện chạm đất đến gốc cây, BC là cây cột điện bị gãy
AB là khoảng cách từ điểm gãy của cây cột điện đến gốc cây. Đặt AB = x (m), x > 0.
\(\Rightarrow BC'=BC=9-x\) (m)
Áp dụng định lý Pitago vào trong tam giác vuông ABC, ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {x^2} + {3^2} = {\left( {9 - x} \right)^2}\\ \Leftrightarrow {x^2} + 9 = 81 - 18x + {x^2}\\ \Leftrightarrow 18x = 72\\ \Leftrightarrow x = {4^{}}\left( {t/m} \right)\end{array}\)
Vậy điểm gãy ngang của cây cột điện cách gốc bằng 4 mét.
khi hình minh họa chưa cho vị trí các điểm các em phải tự chọn tên các điễm để giải. Hình vẽ minh họa có thể chưa phục vụ được cho bài toán thì các em có thể vẽ lại hình vẽ minh họa cho việc giải bài toán dễ dàng hơn (ý 2 trong đề).
Đáp án cần chọn là: C
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
