Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), cung tròn có phương trình

Câu hỏi số 260338:

Vận dụng

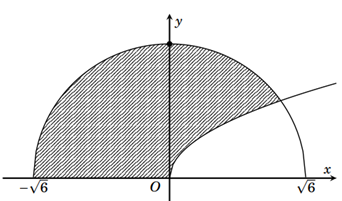
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y = \sqrt {6 - {x^2}} \) \(\left( -\,\sqrt{6}\le x\le \sqrt{6} \right)\) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay sinh bởi khi quay hình phẳng \(D\) quanh trục \(Ox\).

\(V=8\pi \sqrt{6}-2\pi \)

\(V = 8\pi \sqrt 6 + \frac{{22\pi }}{3}\).

\(V = 8\pi \sqrt 6 - \frac{{22\pi }}{3}\).

D. \(V=4\pi \sqrt{6}+\frac{22\pi }{3}\).

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:260338

Phương pháp giải

Chia nhỏ miền để tính thể tích của khối tròn xoay

Giải chi tiết

Cách 1. Cung tròn khi quay quanh \(Ox\) tạo thành một khối cầu có thể tích \(V=\frac{4}{3}\pi {{\left( \sqrt{6} \right)}^{3}}=8\pi \sqrt{6}\).

Thể tích nửa khối cầu là \({{V}_{1}}=4\pi \sqrt{6}\). Xét phương trình:

\(\sqrt x = \sqrt {6 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
{x^2} + x - 6 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
\left[ \begin{array}{l}
x = 2\\
x = - 3
\end{array} \right.
\end{array} \right. \Leftrightarrow x = 2.\)

Thể tích khối tròn xoay có được khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị các hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y=\sqrt{6-{{x}^{2}}}\), và hai đường thẳng \(x=0,\,\,x=2\) quanh \(Ox\) là:

\({{V}_{2}}=\pi \int\limits_{0}^{2}{\left( 6-{{x}^{2}}-x \right)\text{d}x}=\left. \pi \left( 6x-\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2} \right) \right|_{0}^{2}=\frac{22\pi }{3}.\).

Vậy thể tích vật thể tròn xoay cần tìm là \(V={{V}_{1}}+{{V}_{2}}=4\pi \sqrt{6}+\frac{22\pi }{3}\).

Cách 2. Cung tròn khi quay quanh \(Ox\) tạo thành một khối cầu có thể tích \({V_1} = \frac{4}{3}\pi {\left( {\sqrt 6 } \right)^3} = 8\pi \sqrt 6 \).

Xét phương trình:

\(\sqrt x = \sqrt {6 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}
x > 0\\
{x^2} + x - 6 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x > 0\\
\left[ \begin{array}{l}
x = 2\\
x = - 3
\end{array} \right.
\end{array} \right. \Leftrightarrow x = 2.\)

Thể tích khối tròn xoay có được khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị các hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y = \sqrt {6 - {x^2}} \) và đường thẳng \(y=0\) quanh \(Ox\) là

\({{V}_{2}}=\pi \int\limits_{0}^{2}{x\text{d}x}+\pi \int\limits_{2}^{\sqrt{6}}{\left( 6-{{x}^{2}} \right)\text{d}x}=\left. \frac{\pi {{x}^{2}}}{2} \right|_{0}^{2}+\left. \pi \left( 6x-\frac{{{x}^{3}}}{3} \right) \right|_{2}^{\sqrt{6}}=2\pi +\frac{12\sqrt{6}-28}{3}\pi =4\pi \sqrt{6}-\frac{22\pi }{3}.\)

Vậy thể tích vật thể tròn xoay cần tìm là \(V = {V_1} - {V_2} = 8\pi \sqrt 6 - \left( {4\pi \sqrt 6 - \frac{{22\pi }}{3}} \right) = 4\sqrt 6 \pi + \frac{{22\pi }}{3}.\)

Chọn D

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.