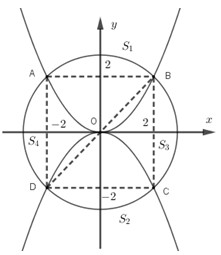
Sân trường có một bồn hoa hình tròn tâm \(O.\) Một nhóm học sinh lớp 12 được giao thiết kế
Sân trường có một bồn hoa hình tròn tâm \(O.\) Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định chia bồn hoa thành bốn phần bởi hai đường parabol có cùng đỉnh \(O\) và đối xứng nhau qua \(O\) (như hình vẽ). Hai đường parabol cắt đường tròn tại bốn điểm \(A,B,C,D\) tạo thành một hình vuông có cạnh bằng \(4m.\) Phần diện tích \({S_1},{S_2}\) dùng để trồng hoa, phần diện tích \({S_3},{S_4}\) dùng để trồng cỏ. Biết kinh phí trồng hoa là \(150.000\) đồng/\(1{m^2},\) kinh phí để trồng cỏ là \(100.000\) đồng/\(1{m^2}.\) Hỏi nhà trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn)
Đáp án đúng là: B
Quảng cáo
+ Từ giả thiết ta viết được phương trình đường tròn và phương trình parabol
+ \({S_1}\) là phần diện tích giới hạn bởi parabol; đường tròn và hai đường thẳng \(x = 2;x = - 2\). Từ đó sử dụng công thức diện tích hình phẳng bằng ứng dụng tích phân để tính \({S_1}.\)
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right)\) và hai đường thẳng \(x = a;x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
+ Từ đó tính \({S_1};{S_2};{S_3};{S_4}\) và tính tiền trồng bồn hoa.
Vì \(ABCD\) là hình vuông cạnh \(4\) nên
\(BD = \sqrt {B{C^2} + C{D^2}} = 4\sqrt 2 \Rightarrow OB = 2\sqrt 2 \) và \(A\left( { - 2;2} \right);B\left( {2;2} \right)\)
Phương trình đường tròn tâm \(O\) bán kính \(r = 2\sqrt 2 \) là \({x^2} + {y^2} = 8 \Rightarrow y = \sqrt {8 - {x^2}} \)
Parabol đi qua hai điểm \(A\left( { - 2;2} \right);B\left( {2;2} \right)\) và có đỉnh \(O\left( {0;0} \right)\) có dạng \(y = a{x^2}\left( {a \ne 0} \right)\)
Khi đó \(2 = a{.2^2} \Rightarrow a = \dfrac{1}{2} \Rightarrow y = \dfrac{1}{2}{x^2}\,\,\left( P \right)\)
Từ đồ thị ta có \({S_1}\) là giới hạn của hai đồ thị hàm số \(y = \sqrt {8 - {x^2}} \) và \(y = \dfrac{1}{2}{x^2}\) và hai đường thẳng \(x = - 2;x = 2.\)
Nên ta có \({S_1} = \int\limits_{ - 2}^2 {\left( {\sqrt {8 - {x^2}} - \dfrac{1}{2}{x^2}} \right)} dx = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} } dx - \left. {\dfrac{1}{6}{x^3}} \right|_{ - 2}^2 = I - \dfrac{8}{3}\)
Xét \(I = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} dx} \) , đặt \(x = 2\sqrt 2 \sin t \Rightarrow dx = 2\sqrt 2 \cos tdt\)
Đổi biến số \(x = - 2 \Rightarrow t = - \dfrac{\pi }{4}\) ; \(x = 2 \Rightarrow t = \dfrac{\pi }{4}\)
Từ đó \(I = \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {\sqrt {8 - 8{{\sin }^2}t} .2\sqrt 2 \cos tdt = } \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {8{{\cos }^2}tdt = } 4\int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt = \left. {4t + 2\sin 2t} \right|_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} = 2\pi + 4} \)
Nên \({S_1} = I - \dfrac{8}{3} = 2\pi + 4 - \dfrac{8}{3} = 2\pi + \dfrac{4}{3}\)
Lại thấy \({S_1} = {S_2};{S_3} = {S_4}\) (vì hai parapol đối xứng nhau qua đình \(O\)), diện tích cả bồn hoa là
\(S = \pi {r^2} = \pi {\left( {2\sqrt 2 } \right)^2} = 8\pi .\)
Từ đó diện tích trồng hoa là \({S_1} + {S_2} = 2{S_1} = 4\pi + \dfrac{8}{3}\,\left( {{m^2}} \right)\)
Diện tích trồng cỏ là \({S_3} + {S_4} = S - \left( {{S_1} + {S_2}} \right) = 4\pi - \dfrac{8}{3}\,\left( {{m^2}} \right)\)
Nên tổng số tiền trồng bồn hoa là \(\left( {4\pi + \dfrac{8}{3}} \right).150000 + \left( {4\pi - \dfrac{8}{3}} \right).100000 \approx 32749256\) đồng.
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
