Trong một môi trường đẳng hướng, không hấp thụ âm cho đường thẳng (d) và hai điểm A, B
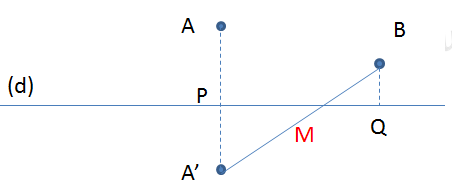
Trong một môi trường đẳng hướng, không hấp thụ âm cho đường thẳng (d) và hai điểm A, B cùng nằm một phía so với (d). Gọi P, Q lần lượt là hình chiếu của A, B lên (d). Tại A có đặt một nguồn âm (xem là nguồn điểm) phát âm đẳng hướng ra không gian với công suất P không đổi. Một thiết bị xác định mức độ cường độ âm M di chuyển trên (d), khi M ở vị trí sao cho tổng (MA+MB) nhỏ nhất thì M đo được mức cường độ âm là 40dB. Giữ nguyên vị trí của M, đặt thêm tại B một nguồn âm giống nguồn âm ở A thì M đo được mức cường độ âm là 60dB. Tỉ số \(\dfrac{{MP}}{{MQ}}\) gần nhất với giá trị nào sau đây?
Đáp án đúng là: D
Quảng cáo
+ Sử dụng hình học phẳng
+ Sử dụng công thức tính cường độ âm: \(I = \dfrac{P}{{4\pi {r^2}}}\)
+ Sử dụng công thức tính mức cường độ âm: \(L = 10\log \dfrac{I}{{{I_0}}}\)
+ Sử dụng công thức hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}}\)
+ Sử dụng tam giác đồng dạng
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( d \right)\) , kẻ \(MA'\) cắt \(\left( d \right)\) tại \(M\)
Ta có điểm M đó chính là điểm tại đó \({\left( {MA + MB} \right)_{\min }}\)
Khi đó \(MA + MB = MA' + MB = A'B\)
+ Khi đặt 1 nguồn âm tại A, mức cường độ âm đo được tại M là:
\({L_1} = 10\log \dfrac{{{I_1}}}{{{I_0}}}\) với \({I_1} = \dfrac{P}{{4\pi {{\left( {AM} \right)}^2}}}\)
+ Khi đặt thêm 1 nguồn âm tại B, mức cường độ âm đo được tại M lúc này:
\({L_2} = 10\log \dfrac{{{I_2}}}{{{I_0}}}\) với \({I_2} = \dfrac{P}{{4\pi M{A^2}}} + \dfrac{P}{{4\pi M{B^2}}}\)
Ta có: \({L_2} - {L_1} = 10\log \dfrac{{{I_2}}}{{{I_1}}} = 10\log \dfrac{{\left( {\dfrac{1}{{A{M^2}}} + \dfrac{1}{{B{M^2}}}} \right)}}{{\dfrac{1}{{A{M^2}}}}}\)
\(\begin{array}{l} \Leftrightarrow 60 - 40 = 10\log \dfrac{{\left( {\dfrac{1}{{A{M^2}}} + \dfrac{1}{{B{M^2}}}} \right)}}{{\dfrac{1}{{A{M^2}}}}}\\ \Rightarrow \dfrac{{\left( {\dfrac{1}{{A{M^2}}} + \dfrac{1}{{B{M^2}}}} \right)}}{{\dfrac{1}{{A{M^2}}}}} = {10^2}\\ \Rightarrow \dfrac{1}{{BM}} = \sqrt {99} \dfrac{1}{{AM}}\\ \Rightarrow AM = \sqrt {99} BM\end{array}\)
Từ hình, ta có \(\Delta PA'M\) đồng dạng với \(\Delta QBM\)
\( \Rightarrow \dfrac{{MP}}{{MQ}} = \dfrac{{A'M}}{{BM}} = \dfrac{{AM}}{{BM}} = \sqrt {99} = 9,49\)
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
