(Học sinh chỉ chọn một trong hai ý: 1 hoặc 2). 1) Cho đa thức \(P\left( x \right) = a\,{x^2} + bx + c\)

Câu hỏi số 402701:

Vận dụng cao

(Học sinh chỉ chọn một trong hai ý: 1 hoặc 2).

1) Cho đa thức \(P\left( x \right) = a\,{x^2} + bx + c\) có tính chất \(P\left( 1 \right);\,P\left( 4 \right);\,P\left( 9 \right)\) là các số hữu tỉ. Chứng minh rằng khi đó \(a,b,c\) là các số hữu tỉ.

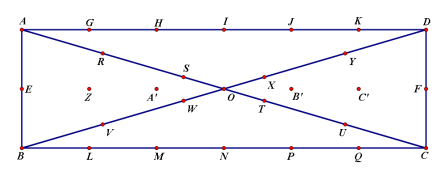
2) Trong một dịp cắm trại, lớp 7A được phân công trang trí một khuôn viên hình chữ nhật có chiều rộng \(7m\) , chiều dài \(24m.\) Việc trang trí cần được thực hiện bằng cách cắm những lá cờ thỏa mãn các yêu cầu sau: Theo chiều rộng của sân, mỗi lá cờ cách nhau 3,5m; theo chiều dài của sân, mỗi lá cờ cách nhau 4m; theo đường chéo của sân, mỗi lá cờ cách nhau 5m; tất cả các góc sân đều được cắm cờ. Hỏi lớp 7A cần dùng bao nhiêu lá cờ để trang trí được khuôn viên theo đúng yêu cầu?

Quảng cáo

Xem lời giải

Câu hỏi:402701

Phương pháp giải

1) Từ dữ kiện đề bài cho, ta lần lượt chứng minh \(a;b;c \in \mathbb{Q}\).

2) Lập luận để tìm ra số lá cờ để trang trí khuôn viên theo đúng yêu cầu.

Giải chi tiết

1) Ta có:

\(P\left( 1 \right) = a + b + c \in \,\mathbb{Q}\,\,\left( 1 \right)\)

\(P\left( 4 \right) = 16a + 4b + c \in \,\mathbb{Q}\,\,\left( 2 \right)\)

\(P\left( 9 \right) = 81a + 9b + c \in \mathbb{Q}\,\,\,\left( 3 \right)\)

Lấy \(\left( 2 \right) - \left( 1 \right)\) \( \Rightarrow 15a + 3b \in \mathbb{Q} \Rightarrow 3\left( {5a + b} \right) \in \mathbb{Q}\,\,\,\,\left( 4 \right)\)

Lấy \(\left( 3 \right) - \left( 1 \right) \Rightarrow 80a + 8b \in \mathbb{Q} \Rightarrow 8\left( {10a + b} \right) \in \mathbb{Q} \Rightarrow 10a + b \in \mathbb{Q}\,\,\,\left( 5 \right)\)

Lấy \(\left( 5 \right) - \left( 4 \right) \Rightarrow 5a \in \mathbb{Q}\,\,\,\,\left( 6 \right)\)

\( \Rightarrow a \in \mathbb{Q}\,\,\,\left( 7 \right)\)

Từ (6) và (4) \( \Rightarrow b \in \mathbb{Q}\,\,\,\left( 8 \right)\)

Từ (8) , (7) và (1) suy ra: \(c \in \mathbb{Q}\)

Vậy \(a;\,b;\,c\) là các số hữu tỉ.

Gọi khuôn viên hình chữ nhật là \(ABCD\) (Hình vẽ).

Độ dài đường chéo \(AC\) và \(BD\) là:

\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{7^2} + {{24}^2}} = \sqrt {625} = 25\left( m \right)\)

Vì \(7:3,5 = 2\) nên mỗi chiều rộng có 2 khoảng (3 lá cờ).

Vì \(24:4 = 6\) nên mỗi chiều dài có 6 khoảng (7 lá cờ).

Vừa chia theo chiều rộng và chiều dài sẽ có \(3.7 = 21\) lá cờ được cắm.

Vì \(25:5 = 5\) nên mỗi đường chéo có 5 khoảng (6 lá cờ).

Nhưng có 2 lá cờ ở 2 góc đã được cắm nên còn lại \(6 - 2 = 4\) lá cờ.

Vì có 2 đường chéo nên số lá cờ cắm theo đường chéo là \(4.2 = 8\) lá cờ.

Vậy lớp 7A cần dùng \(21 + 8 = 29\) lá cờ để trang trí khuôn viên theo đúng yêu cầu.

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link