Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ
Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua một sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sĩ 1km theo đường chim bay và chiến sĩ cách bờ bên kia 100m.
Đáp án đúng là: D
Quảng cáo
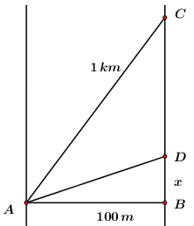
Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.
Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.
Ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {{{1000}^2} - {{100}^2}} = 300\sqrt {11} \,\,\left( m \right).\)
Đặt \(BD = x\,\,\,\left( m \right),\,\,\left( {0 < x < 300\sqrt {11} } \right).\)
\( \Rightarrow \) Quãng đường chiến sĩ phải bơi là: \(AD = \sqrt {A{B^2} + B{D^2}} = \sqrt {{x^2} + {{100}^2}} \,\,\left( m \right).\)
Quãng đường chiến sĩ phải chạy bộ là: \(CD = BC - BD = 300\sqrt {11} - x\,\,\left( m \right).\)
\( \Rightarrow \) Thời gian chiến sĩ đến được mục tiêu là: \(t = \dfrac{{AD}}{a} + \dfrac{{DC}}{{3a}}\)
Tìm \(x\) để \(t\left( x \right)\) đạt \(Min\) rồi suy ra quãng đường chiễn sĩ phải bơi.
Gọi vận tốc của chiến sĩ khi bơi là \(a\,\,\left( {m/s} \right),\,\,\left( {a > 0} \right).\)
\( \Rightarrow \) Vận tốc của chiến sĩ khi chạy bộ là: \(3a\,\,\left( {m/s} \right).\)
Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.
Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.
Ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {{{1000}^2} - {{100}^2}} = 300\sqrt {11} \,\,\left( m \right).\)
Đặt \(BD = x\,\,\,\left( m \right),\,\,\left( {0 < x < 300\sqrt {11} } \right).\)
\( \Rightarrow \) Quãng đường chiến sĩ phải bơi là: \(AD = \sqrt {A{B^2} + B{D^2}} = \sqrt {{x^2} + {{100}^2}} \,\,\left( m \right).\)
Quãng đường chiến sĩ phải chạy bộ là: \(CD = BC - BD = 300\sqrt {11} - x\,\,\left( m \right).\)
\( \Rightarrow \) Thời gian chiến sĩ đến được mục tiêu là:
\(\begin{array}{l}t = \dfrac{{AD}}{a} + \dfrac{{DC}}{{3a}} = \dfrac{{\sqrt {{x^2} + {{100}^2}} }}{a} + \dfrac{{300\sqrt {11} - x}}{{3a}}\\\,\,\, = \dfrac{1}{{3a}}\left( {3\sqrt {{x^2} + {{100}^2}} + 300\sqrt {11} - x} \right)\end{array}\)
Xét hàm số: \(f\left( x \right) = 3\sqrt {{x^2} + {{100}^2}} - x + 300\sqrt {11} \) trên \(\left( {0;\,\,300\sqrt {11} } \right)\) ta có:
\(f'\left( x \right) = \dfrac{{3x}}{{\sqrt {{x^2} + {{100}^2}} }} - 1\) \( \Rightarrow f'\left( x \right) = 0\)
\( \Leftrightarrow 3x = \sqrt {{x^2} + {{100}^2}} \) \( \Leftrightarrow 9{x^2} = {x^2} + {100^2}\)
\( \Leftrightarrow 8{x^2} = {100^2}\) \( \Leftrightarrow x = 25\sqrt 2 \,\,\left( {tm} \right)\)
Quãng đường bơi mà chiến sĩ phải bơi để đến được mục tiêu nhanh nhất là: \(AD = \sqrt {{x^2} + {{100}^2}} = \sqrt {(25\sqrt 2)^2 + 100^2} \) \( = 75\sqrt 2 \,\,m.\)
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
