Một quả đạn khối lượng 10kg đang bay thẳng đứng xuống dưới với vận tốc 85m/s đến

Câu hỏi số 542286:

Vận dụng cao

Một quả đạn khối lượng 10kg đang bay thẳng đứng xuống dưới với vận tốc 85m/s đến điểm M thì nổ thành hai mảnh. Mảnh thứ nhất có khối lượng 6kg bay với vận tốc 64m/s. Bỏ qua mọi sức cản. Lấy \(g = 10m/{s^2}\).

a) Ngay sau khi nổ nếu mảnh thứ nhất bay theo phương ngang. Tính độ lớn vận tốc của mảnh thứ hai khi đó.

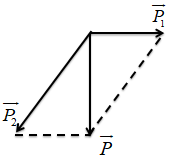
b) Ngay sau khi nổ, nếu mảnh thứ nhất bay theo chếch lên, hợp với phương ngang góc \({30^0}\).

+ Tính độ lớn vận tốc của mảnh thứ hai khi đó.

+ Tính độ cao nhất mà mảnh thứ nhất có thể lên đến so với điểm M.

Quảng cáo

Xem lời giải

Câu hỏi:542286

Phương pháp giải

Áp dụng định luật bảo toàn động lượng: Động lượng của một hệ cô lập là một đại lượng bảo toàn.

Động lượng: \(p = mv\)

Công thức liên hệ s,v,a: \({v^2} - v_0^2 = 2a.s\)

Giải chi tiết

Khi đạn nổ, lực tác dụng của không khí rất nhỏ so với nội lực nên được coi như là một hệ kín.

a) Viên đạn đang bay thẳng đứng, nổ thành 2 mảnh, mảnh thứ nhất bay theo phương ngang nên suy ra \(\vec p \bot \overrightarrow {{p_1}} \)

Áp dụng ĐLBT động lượng ta có: \(\vec p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)

\( \Leftrightarrow p_2^2 = {p^2} + p_1^2 \Leftrightarrow {p_2} = \sqrt {{{\left( {m.v} \right)}^2} + {{\left( {{m_1}.{v_1}} \right)}^2}} \)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {10.85} \right)}^2} + {{\left( {6.64} \right)}^2}} = 932,7\left( {kg.m/s} \right)\)

Độ lớn vận tốc của mảnh thứ hai là:

\({v_2} = \dfrac{{{p_2}}}{{{m_2}}} = \dfrac{{{p_2}}}{{m - {m_1}}} = \dfrac{{932,7}}{{10 - 6}} = 233m/s\)

b) Nếu mảnh thứ nhất chếch lên hợp với phương ngang góc \({30^0}\)

\( \Rightarrow \left( {\vec p,\overrightarrow {{p_1}} } \right) = 90 + 30 = {120^0} \Rightarrow \widehat {O{p_1}{p_2}} = {60^0}\)

Khi đó, ta có:\(p_2^2 = {p^2} + p_1^2 - 2p.{p_1}.\cos {60^0}\)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {m.v} \right)}^2} + {{\left( {{m_1}.{v_1}} \right)}^2} - 2mv.{m_1}{v_1}.\cos 60} \)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {10.85} \right)}^2} + {{\left( {6.64} \right)}^2} - 2.10.85.6.64.\dfrac{1}{2}} \)

\( \Leftrightarrow {p_2} = 737,3\left( {kg.m/s} \right)\)

Độ lớn vận tốc của mảnh thứ hai khi đó là:

\({v_2} = \dfrac{{{p_2}}}{{{m_2}}} = \dfrac{{737,3}}{{10 - 6}} = 184\left( {m/s} \right)\)

Khi lên đến vị trí cao nhất thì vận tốc của vật bằng 0. Ta có:

\({v^2} - v_1^2 = 2gh \Leftrightarrow h = \dfrac{{{0^2} - {{64}^2}}}{{2.\left( { - 10} \right)}} = 204,8m\)

Vậy độ cao nhất mà mảnh thứ nhất có thể lên đến so với điểm M là 204,8m.

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10