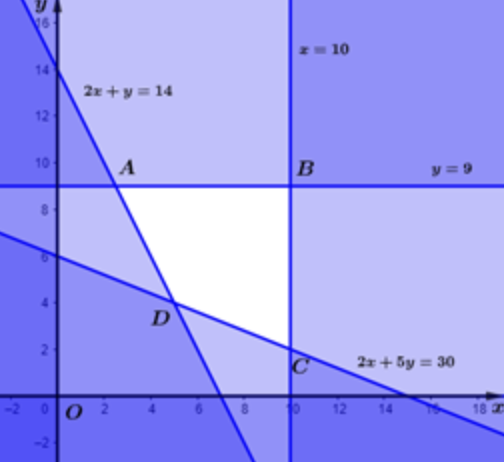
Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và
Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Tính chi phí thấp nhất để mua nguyên liệu chiết xuất ít nhất 140 kg chất A và 9 kg chất B?
Đáp án đúng là: A
Quảng cáo
Gọi x, y lần lượt là số tấn nguyên liệu loại I và II (Đơn vị: kg, ĐK:\(x,y \ge 0\)).
Số tiền mua nguyên liệu là F = 4x + 3y.
Số kg chất A chiết xuất được là 20x + 10y (kg).
Số kg chất A chiết xuất được là 0,6x + 1,5y (kg).
Theo bài ra ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\20x + 10y \ge 140\\0,6x + 1,5y \ge 9\end{array} \right.\).
Miền nghiệm của hệ bất phương trình là tứ giác ABCD kể cả miền trong.
Ta có: \(A\left( {\dfrac{5}{2};9} \right)\), B(10;9), C(10;2), D(5;4).
Ta tính giá trị của biểu thức F = 4x + 3y tại tất cả các đỉnh của tứ giác ABCD, ta có:
F(A) = 32
F(B) = 67
F(C) = 46
F(D) = 32
Vậy chi phí mua nguyên liệu ít nhất là 32 triệu đồng.
Đáp án cần chọn là: A
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
