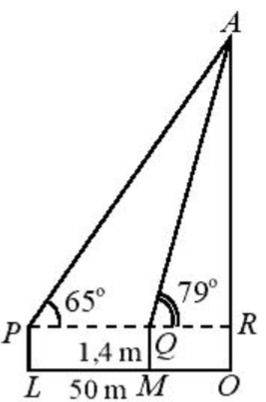
Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng

Câu hỏi số 586252:

Vận dụng

Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng \(\angle RQA = {79^0}\), người đó lùi ra xa một khoảng cách LM = 50 m thì nhìn thấy đỉnh toà nhà với góc nâng \(\angle RPA = {65^0}\). Hãy tính chiều cao của toà nhà (làm tròn đến chữ số thập phân thứ nhất), biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4m.

A. 135,8m

B. 183,5m

C. 158,3m

D. 185,3m

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:586252

Phương pháp giải

Tính PR và QR theo h = AR và \(\tan \alpha = \tan {65^0},\,\,\tan \beta = \tan {79^0}\).

Sử dụng d = PQ = PR – QR, tính d.

Tính chiều cao tòa nhà bằng d + RO.

Giải chi tiết

Đặt d = PQ = LM = 50m, h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.

Ta có: \(\angle APR = \alpha = {65^0},\,\,\angle AQR = \beta = {79^0}\).

Gọi \({d_1} = PR = \dfrac{h}{{\tan \alpha }},\,\,{d_2} = QR = \dfrac{h}{{\tan \beta }}\), ta có:

\(\begin{array}{l}d = {d_1} - {d_2} = \dfrac{h}{{\tan \alpha }} - \dfrac{h}{{\tan \beta }} = h\left( {\dfrac{1}{{\tan \alpha }} - \dfrac{1}{{\tan \beta }}} \right)\\ \Rightarrow h = \dfrac{d}{{\dfrac{1}{{\tan \alpha }} - \dfrac{1}{{\tan \beta }}}} = \dfrac{{50}}{{\dfrac{1}{{\tan {{65}^0}}} - \dfrac{1}{{\tan {{79}^0}}}}} \approx 183,9\,\,\left( m \right)\end{array}\)

Vậy chiều cao của tòa nhà là AR + RO \( \approx 183,9 + 1,4 = 185,3\,\,\left( m \right)\).

Đáp án cần chọn là: D

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10