Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người

Câu hỏi số 637997:

Vận dụng

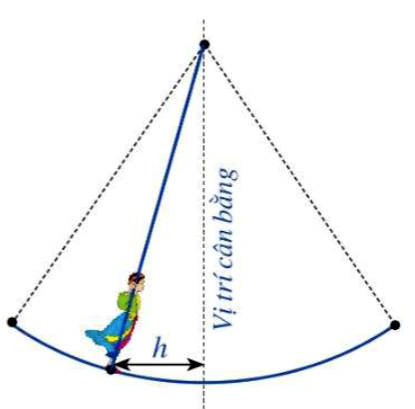
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách \(h\) (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với \(t \ge 0\)) bởi hệ thức \(h = \left| d \right|\) với \(d = 3\cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại. Vào thời gian t nào thì khoảng cách h là 3m, 0m?

Quảng cáo

Xem lời giải

Câu hỏi:637997

Phương pháp giải

Giải phương trình lượng giác cơ bản đặc biệt:

\(\begin{array}{l}\cos x = 1 \Leftrightarrow x = k2\pi \\\cos x = - 1 \Leftrightarrow x = \pi + k2\pi \\\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \end{array}\)

Giải chi tiết

+) h = 3

\(\begin{array}{l} \Leftrightarrow \left| {3\cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right]} \right| = 3\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right] = 1\\\cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right] = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\dfrac{\pi }{3}\left( {2t - 1} \right) = k2\pi \\\dfrac{\pi }{3}\left( {2t - 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2t - 1 = 6k\\2t - 1 = 3 + 6k\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = 3k + \dfrac{1}{2}\\t = 3k + 2\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

TH1: \(t = 3k + \dfrac{1}{2}\), do \(t \ge 0 \Leftrightarrow 3k + \dfrac{1}{2} \ge 0 \Leftrightarrow k \ge - \dfrac{1}{6}\).

Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;...} \right\}\).

=> Tại các thời điểm \(t = 3k + \dfrac{1}{2},\,\,k \in \mathbb{N}\) thì h = 3.

TH2: \(t = 3k + 2\), do \(t \ge 0 \Leftrightarrow 3k + 2 \ge 0 \Leftrightarrow k \ge - \dfrac{2}{3}\).

Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;...} \right\}\).

=> Tại các thời điểm \(t = 3k + 2,\,\,k \in \mathbb{N}\) thì h = 3.

Vậy tại các thời điểm \(t = 3k + \dfrac{1}{2},\,\,k \in \mathbb{N}\) hoặc \(t = 3k + 2,\,\,k \in \mathbb{N}\) thì h = 3.

+) h = 0

\(\begin{array}{l} \Rightarrow \cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \dfrac{\pi }{3}\left( {2t - 1} \right) = \dfrac{\pi }{2} + k\pi \\ \Leftrightarrow 2t - 1 = \dfrac{3}{2} + 3k\\ \Leftrightarrow t = \dfrac{5}{4} + \dfrac{3}{2}k\end{array}\)

Do \(t \ge 0 \Leftrightarrow \dfrac{5}{4} + \dfrac{3}{2}k \ge 0 \Leftrightarrow k \ge - \dfrac{5}{6}\)

Mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;...} \right\}\).

=> Tại các thời điểm \(t = \dfrac{5}{4} + \dfrac{3}{2}k,\,\,k \in \mathbb{N}\) thì h = 0.

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.