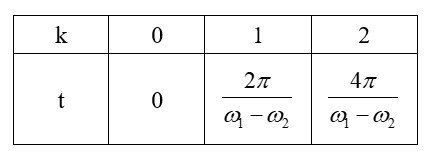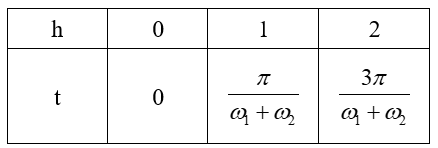Hai con lắc đơn có chiều dài \({l_1} = 100\,\,cm\) và \({l_2}\) (với \({l_2} < {l_1}\)) được treo

Câu hỏi số 640138:

Vận dụng cao

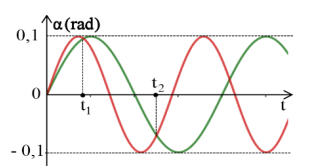
Hai con lắc đơn có chiều dài \({l_1} = 100\,\,cm\) và \({l_2}\) (với \({l_2} < {l_1}\)) được treo tại cùng một nơi có \(g = 10\,\,m/{s^2}\). Bỏ qua lực cản không khí, lấy \({\pi ^2} = 10\). Ban đầu, từ vị trí cân bằng đồng thời truyền cho hai quả cầu vận tốc nằm ngang, cùng chiều để chúng dao động điều hòa trong hai mặt phẳng song song với nhau. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ góc của mỗi con lắc theo thời gian. Biết \({t_2} - {t_1} = \dfrac{8}{9}\,\,s\). Không kể lúc truyền vận tốc, tại thời điểm mà hai dây treo song song với nhau lần thứ 2023 thì tốc độ của con lắc có chiều dài \({l_2}\) là

A. 18,1 cm/s.

B. 21,5 cm/s.

C. 5,6 cm/s.

D. 14,0 cm/s.

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:640138

Phương pháp giải

Viết phương trình li độ góc của hai con lắc

Hai dây treo ở vị trí song song với nhau khi \({\alpha _1} = {\alpha _2}\)

Biện luận theo họ nghiệm suy ra giá trị t₁, t₂trên đồ thị.

Để trạng thái hai dây treo song song lặp lại thì \(\Delta t = {n_1}{T_1} = {n_2}{T_2}\)

Viết phương trình vận tốc của con lắc thứ hai, thay t vào tính được tốc độ.

Giải chi tiết

Tần số góc của con lắc thứ nhất là: \({\omega _1} = \sqrt {\dfrac{g}{{{l_1}}}} = \sqrt {\dfrac{{10}}{1}} = \pi \) (rad/s)

Vì \({l_2} > {l_1} \Rightarrow {\omega _2} > {\omega _1}\)

Phương trình dao động của hai con lắc là:

\(\left\{ \begin{array}{l}{\alpha _1} = 0,1.\cos \left( {{\omega _1}t - \dfrac{\pi }{2}} \right)\\{\alpha _2} = 0,1.\cos \left( {{\omega _2}t - \dfrac{\pi }{2}} \right)\end{array} \right.\)

Hai dây treo ở vị trí song song với nhau khi \({\alpha _1} = {\alpha _2}\)

\(\begin{array}{l}\left[ \begin{array}{l}{\omega _1}t - \dfrac{\pi }{2} = {\omega _2}t - \dfrac{\pi }{2} + 2k\pi \\{\omega _1}t - \dfrac{\pi }{2} = - {\omega _2}t + \dfrac{\pi }{2} + 2h\pi \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\left( {{\omega _1} - {\omega _2}} \right)t = 2k\pi \\\left( {{\omega _1} + {\omega _2}} \right)t = \pi + 2h\pi \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}t = \dfrac{{2k\pi }}{{{\omega _1} - {\omega _2}}}\\t = \dfrac{{\pi + 2h\pi }}{{{\omega _1} + {\omega _2}}}\end{array} \right.\end{array}\)

Ta xét bảng giá trị:

+ Họ nghiệm \(t = \dfrac{{2k\pi }}{{{\omega _1} - {\omega _2}}}\)

Họ nghiệm \(t = \dfrac{{\pi + 2h\pi }}{{{\omega _1} + {\omega _2}}}\)

Từ bảng giá trị ta thấy:

\({t_1} = \dfrac{\pi }{{{\omega _1} + {\omega _2}}};{t_2} = \dfrac{{3\pi }}{{{\omega _1} + {\omega _2}}}\)

\(\begin{array}{l}{t_2} - {t_1} = \dfrac{8}{9}\,\,\left( s \right)\\ \Rightarrow \dfrac{{2\pi }}{{\pi + {\omega _2}}} = \dfrac{8}{9} \Rightarrow {\omega _2} = \dfrac{{5\pi }}{4}\,\,\left( {rad/s} \right)\end{array}\)

Chu kì của con lắc thứ hai là:

\({T_2} = \dfrac{{2\pi }}{{{\omega _2}}} = \dfrac{{2\pi }}{{5\pi /4}} = 1,6\,\,\left( s \right)\)

Để trạng thái hai dây song song lặp lại thì:

\(\begin{array}{l}\Delta t = {n_1}{T_1} = {n_2}{T_2}\\ \Rightarrow \dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{1,6}}{2} = \dfrac{4}{5}\\ \Rightarrow \Delta t = 4{T_1} = 5{T_2} = 8\,\,\left( s \right)\end{array}\)

Ta cần tính xem trong khoảng thời gian \(\Delta t\) có bao nhiêu lần 2 con lắc gặp nhau

Từ \(\left[ {\begin{array}{*{20}{l}}{t = \dfrac{{k2\pi }}{{5\pi /4 - \pi }} = 8k}\\{t = \dfrac{{\pi + h2\pi }}{{5\pi /4 + \pi }} = \dfrac{4}{9} + \dfrac{{8h}}{9}}\end{array}} \right.\) (với \(0 \le t \le 8\))

\( \Rightarrow \left[ \begin{array}{l}k = 1\\h = 0;1;2;3;4;5;6;7;8\end{array} \right.\)

→ cứ \({T_{12}} = 8\,\,s\) thì có 10 lần hai con lắc gặp nhau

\(2013 = 201.10 + 3 \Rightarrow {t_3} = \dfrac{4}{9} + \dfrac{{8.2}}{9} = \dfrac{{20}}{9}\,\,\left( s \right)\)

Phương trình li độ cong của con lắc thứ 2 là:

\({s_2} = {l_2}{\alpha _2} = {l_2}{\alpha _0}\sin \left( {{\omega _2}t} \right)\)

Phương trình vận tốc của con lắc thứ hai là:

\({v_2} = {s_2}^\prime = {l_2}{\alpha _0}{\omega _2}\cos \left( {{\omega _2}t} \right)\)

Vậy sau \(\dfrac{{20}}{9}\,\,s\) thì:

\({v_2} = 0,64 \cdot 0,1 \cdot \dfrac{{5\pi }}{4} \cdot \cos \left( {\dfrac{{5\pi }}{4} \cdot \dfrac{{20}}{9}} \right) \approx - 0,193\,\,\left( {m/s} \right)\)

Độ lớn vận tốc của con lắc thứ hai là:

0,193 m/s = 13,9 cm/s

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.