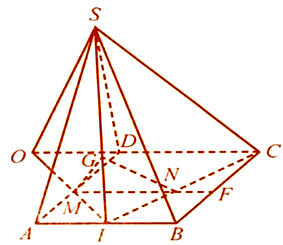
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình bình hành. Gọi \(G\) là trọng tâm của tam giác

Câu hỏi số 650515:

Vận dụng

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình bình hành. Gọi \(G\) là trọng tâm của tam giác \(SAB,I\) là trung điểm của \(AB\) và \(M\) là điểm thuộc cạnh \(AD\) sao cho \(AM = \dfrac{1}{3}AD\). Đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(CI\) tại \(N\). Chứng minh:

a) \(NG//\left( {SCD} \right)\);

b) \(MG//\left( {SCD} \right)\).

Quảng cáo

Xem lời giải

Câu hỏi:650515

Giải chi tiết

a) Gọi \(F\) là giao điểm của \(MN\) và \(BC\).

Ta có \(MN//AB\), suy ra \(NF//BI\) (vì \(F \in MN,I \in AB\) ).

Trong tam giác \(CIB\) có \(NF//BI\), nên theo định lí Thalès ta có: \(\dfrac{{NI}}{{CI}} = \dfrac{{BF}}{{BC}} = \dfrac{1}{3}\).

Trong tam giác \(SAB\), ta có \(G\) là trọng tâm nên \(\dfrac{{GI}}{{SI}} = \dfrac{1}{3}\).

Trong tam giác \(SIC\), ta có \(\dfrac{{GI}}{{SI}} = \dfrac{{NI}}{{CI}} = \dfrac{1}{3}\), suy ra \(NG//SC\) (định lí Thalès đảo). Do đó \(NG//\left( {SDC} \right)\).

b) Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(O\) là giao điểm của \(MI\) và \(DC\).

Trong tam giác \(OCI\) có \(MN//OC\), suy ra \(\dfrac{{MI}}{{OI}} = \dfrac{{IN}}{{IC}} = \dfrac{1}{3}\) (theo định lí Thalès).

Mà \(\dfrac{{IG}}{{SI}} = \dfrac{1}{3}(G\) là trọng tâm của tam giác \(SAB)\).

Do đó, trong tam giác \(SOI\) có \(\dfrac{{MI}}{{OI}} = \dfrac{{IG}}{{SI}} = \dfrac{1}{3}\), suy ra \(MG//SO\) (định lí Thalès đảo).

Do đó \(MG//\left( {SDC} \right)\).

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.