Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), biết \(AD = 2a,AB = BC =

Câu hỏi số 671762:

Vận dụng

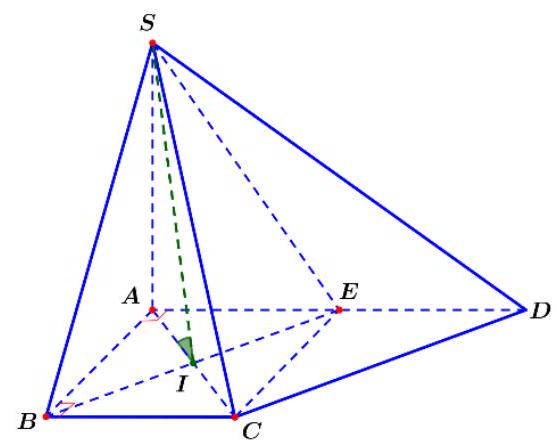
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), biết \(AD = 2a,AB = BC = a\) , cạnh bên \(SA\) vuông góc với mặt đáy và \(SA = \dfrac{{a\sqrt 6 }}{2}\). Gọi \(E\) là trung điểm của \(AD\). Tính số đo của góc phẳng nhị diện \(\left[ {S,BE,A} \right]\).

Quảng cáo

Xem lời giải

Câu hỏi:671762

Phương pháp giải

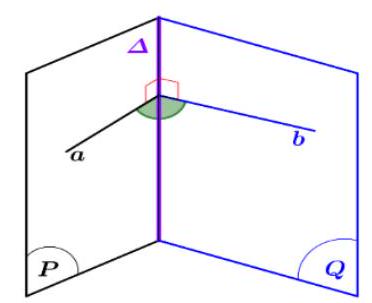
Ta xác định góc nhị diện tạo bởi hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) theo 3 bước:

Bước 1: Tìm giao tuyến \({\rm{\Delta }} = \left( P \right) \cap \left( Q \right)\).

Bước 2: Tìm \(a \subset \left( P \right):a \bot {\rm{\Delta }}\) và \(b \subset \left( Q \right):b \bot {\rm{\Delta }}\).

Bước 3: Kết luận \(\left[ {P,{\rm{\Delta }},Q} \right]\)

Giải chi tiết

Nhận xét: \(ABCE\) là hình vuông cạnh bằng \(a\).

Gọi \(I = AC \cap BE\).

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BE \bot AI}\\{BE \bot SA}\end{array} \Rightarrow BE \bot \left( {SAI} \right) \Rightarrow BE \bot SI} \right.\).

Khi đó \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBE} \right) \cap \left( {ABE} \right) = BE}\\{AI \bot BE}\\{SI \bot BE}\end{array} \Rightarrow \left[ {S,BE,A} \right] = \widehat {SIA}} \right.\)

Xét vuông tại \(A\), ta có:

\({\rm{tan}}\widehat {SIA} = \dfrac{{SA}}{{IA}} = \dfrac{{a\sqrt 6 }}{2}:\dfrac{{a\sqrt 2 }}{2} = \sqrt 3 \Rightarrow \widehat {SIA} = {60^ \circ }\)

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.