Dựa vào thông tin dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu từ câu 26
Dựa vào thông tin dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu từ câu 26 đến câu 28 .
Một cái thùng hình trụ không có nắp, bên trong thùng có chứa một lượng nước. Một cái nút chai nhấp nhô lên xuống trong thùng (xem Hình 1), biết rằng khoảng cách từ tâm nút chai đến đáy thùng được cho bởi công thức \(s(t) = 50 + \cos (\pi t){\rm{cm}}\), theo thời gian t giây \((t \ge 0)\).
Trả lời cho các câu 1, 2, 3 dưới đây:
Nút chai gần với đáy nhất tại thời điểm nào dưới đây?
Đáp án đúng là: A
Nút chai gần với đáy nhất tức là \(s(t) = 50 + \cos (\pi t){\rm{cm}}\)đạt GTNN
Đáp án cần chọn là: A
Thứ tự thời gian (tính bằng đơn vị giây) nào sau đây có vận tốc tức thời tương ứng của nút chai giảm dần?
Đáp án đúng là: B
Tính đạo hàm của \(v\left( t \right) = s'\left( t \right)\) và tính \(v\left( t \right)\) tại \(t = \dfrac{1}{2},\dfrac{1}{4},\dfrac{3}{2}\)
Đáp án cần chọn là: B
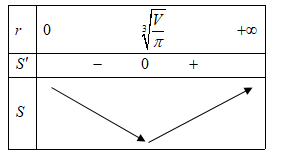
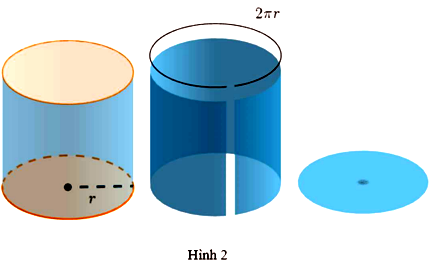
Ông A định làm một cái thùng hình trụ không nắp như trên bằng kim loại có thể tích cho trước. Để giảm thiểu lượng kim loại được sử dụng, ông A cần làm cái thùng sao cho diện tích bề mặt phải càng nhỏ càng tốt (Hình 2). Chiều cao của thùng bằng bao nhiêu lần bán kính đáy thì tiết kiệm kim loại nhất?
Đáp án đúng là: A
Gọi bán kính đáy là r, chiều cao h
\(V = \pi {r^2}.h \Rightarrow h = \dfrac{V}{{\pi {r^2}}}\)
\(\begin{array}{l}S = 2\pi r.h + \pi {r^2} = \dfrac{{2\pi r.V}}{{\pi {r^2}}} + \pi {r^2} = \pi {r^2} + \dfrac{{2V}}{r}\\ \Rightarrow S' = 2\pi r - \dfrac{{2V}}{{{r^2}}} = 0 \Leftrightarrow \dfrac{{2V}}{{{r^2}}} = 2\pi r \Leftrightarrow {r^3} = \dfrac{V}{\pi } \Leftrightarrow r = \sqrt[3]{{\dfrac{V}{\pi }}}\end{array}\)
\( \Rightarrow {S_{\min }} \Leftrightarrow {r^3} = \dfrac{V}{\pi } \Rightarrow V = \pi {r^3} \Rightarrow h = \dfrac{{\pi {r^3}}}{{\pi {r^2}}} = r \Rightarrow \dfrac{h}{r} = 1\)
Đáp án cần chọn là: A
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
