Kinh viễn vọng không gian Hubble được đưa vào vũ trụ ngày \(24 / 4 / 1990\) bằng
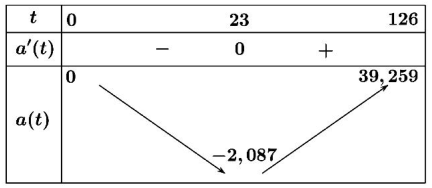
Kinh viễn vọng không gian Hubble được đưa vào vũ trụ ngày \(24 / 4 / 1990\) bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm \(t=0(s)\) cho đến khi tên lửa đẩy được phóng đi tại thời điểm \(t=126(\mathrm{~s})\) cho bởi hàm số sau đây: \(v(t)=0,001302 t^3-0,09029 t^2+23,(\mathrm{v}\) được tính bằng \(\mathrm{ft} / \mathrm{s}, 1\) feet \(=0,3048 \mathrm{~m})\). Gọi \((a ; b)\) là khoảng thời gian gia tốc của tàu con thoi sẽ tăng tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi. Tính \(T=a+b\) ?
Đáp án đúng là:
Quảng cáo
Xét hàm số vận tốc của tàu con thoi \(v(t)=0,001302 t^3-0,09029 t^2+23\) với \(t \in[0 ; 126]\).
Gia tốc của tàu con thoi là \(a(t)=v^{\prime}(t)=0,003906 t^2-0,18058 t\).
Ta có \(a^{\prime}(t)=0,007812 t-0,18058=0 \Leftrightarrow t \approx 23\).
Bảng biến thiên của hàm số \(a(t)\) như sau:
Vậy gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian \((23 s ; 126 s)\) tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi.
Do đó: \(T=a+b=23+126=149\).
Đáp án cần điền là: 149
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
