Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Toán 10

Trước một tòa nhà, người ta làm một cái hồ bơi có dạng hình

Câu hỏi số 739196:
Vận dụng

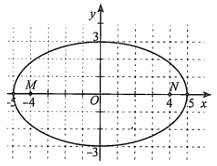
Trước một tòa nhà, người ta làm một cái hồ bơi có dạng hình elip với độ dài hai bán trục lần lượt là \(3 m\) và \(5 m\). Xét hệ trục tọa độ \(Oxy\) (đơn vị trên các trục là mét) có hai trục tọa độ chứa hai trục của elip, gốc tọa độ \(O\) là tâm của elip (hình)

Đúng Sai
a) Phương trình chính tác của đường elip là: \(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\).
b) Xét các điểm \(M, N\) cùng thuộc trục lớn của elip và đều cách \(O\) một khoảng bằng 4 m về hai phía của \(O\). Tổng khoảng cách từ mọi điểm trên đường elip đến \(M\) và \(N\) luôn bằng 10 m
c) Một người đứng ở vị trí \(P\) cách \(O\) một khoảng bằng 6 m . Người đó đứng ở trong hồ
d) Xét vị trí \(C\) trên mép hồ cách trục lớn một khoảng bẳng 2 m . Khi đó vị trí \(C\) cách trục nhỏ một khoảng bằng \(\dfrac{5}{3} m\)

Đáp án đúng là: Đ; Đ; S; S

Quảng cáo

Xem lời giải
Câu hỏi:739196
Giải chi tiết

a) Đúng: Phương trình chính tắc của đường elip là:

\(\dfrac{x^2}{5^2}+\dfrac{y^2}{3^2}=1 \Leftrightarrow \dfrac{x^2}{25}+\dfrac{y^2}{9}=1\).

b) Đúng: Ta có: \(a=5, b=3\) nên \(c^2=a^2-b^2=25-9=16\), suy ra \(c=4\).

Các tiêu điểm của elip có toạ độ là \((-4 ; 0)\) và \((4 ; 0)\).

Vậy \(M\) và \(N\) chính là các tiêu điểm của elip.

Vì vậy, tổng khoảng cách từ mọi điểm trên đường elip đến \(M\) và \(N\) luôn bằng \(2 a=10 \mathrm{~m}\) không đổi.

c) Sai: Gọi giao điểm của đường thẳng \(O P\) và elip là \(Q\).

Vì độ dài bán trục lớn là 5 m nên \(O Q \leq 5\).

Suy ra \(O Q<O P=6 \mathrm{~m}\).

Vậy vị trí \(P\) ở ngoài hồ.

d) Sai: Giả sử \(C\left(x_0 ; y_0\right)\).

Ta có: \(\left\{\begin{array}{l}\dfrac{x_0^2}{25}+\dfrac{y_0^2}{9}=1 \\ \left|y_0\right|=2\end{array} \right.\)

\(\Rightarrow\left\{\begin{array}{l}\dfrac{x_0^2}{25}+\dfrac{4}{9}=1 \\ \left|y_0\right|=2\end{array} \right.\)

\(\Rightarrow\left\{\begin{array}{l}\left|x_0\right|=\dfrac{5 \sqrt{5}}{3} \\ \left|y_0\right|=2\end{array}\right.\)

Vậy \(C\) cách trục nhỏ một khoảng bằng \(\dfrac{5 \sqrt{5}}{3} m\).

Đáp án cần chọn là: Đ; Đ; S; S

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn