Người ta cần lắp một camera phía trên sân bóng để phát sóng

Câu hỏi số 740136:

Vận dụng

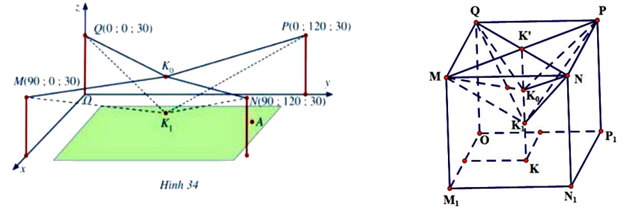
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục tọa độ Oxyz (đơn vị độ dài trên mỗi trục là 1 m ), các đỉnh của bốn chiếc cột lần lượt là các điểm \(M(90;0;30),N(90;120;30),P(0;120;30),Q(0;0;30)\) (Hình 34 ). Giả sử \({K_0}\) là vị trí ban đầu của camera có cao độ bằng 25 và \({K_0}M = {K_0}N = {K_0}P = {K_0}Q\). Để theo dõi quả bóng đến vị trí \(A\), camera được hạ thấp theo phương thẳng đứng xuống điểm \({K_1}\) có cao độ bằng 19 (Nguồn: https://www.abiturloesumg.de; Abitur Bayern 2016 Geometrie VI).

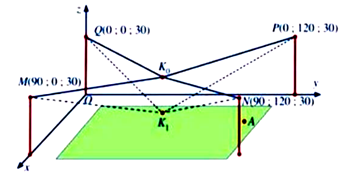
Biết rằng vecto \(\overrightarrow {{K_0}{K_1}} \) có tọa độ là \((a;b;c);a,b,c \in \mathbb{R}\). Khi đó \(a + b + c\) bằng bao nhiêu?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:740136

Giải chi tiết

Ta mô tả lại được hình vẽ sau

Gọi \({M_1},{N_1},{P_1},K\) lần lượt là hình chiếu của \(M,N,P,{K_0}\) lên mặt phẳng \((Oxy)\).

Ta thấy \(MNPQ.{M_1}{N_1}{P_1}O\) là hình hộp chữ nhật.

Gọi \({K^\prime }\) là giao hai đường chéo MP và NQ.

Khi đó \(K'Q = K'P = K'N = K'M\).

Vì \({K_0}M = {K_0}N = {K_0}P = {K_0}Q\) và camera được hạ thấp theo phương thẳng đứng từ điểm \({K_0}\) xuống điểm \({K_1}\) nên các điểm \(K',{K_0},{K_1},K\) thẳng hàng.

Khi đó, các điểm \({K^\prime },{K_0},{K_1},K\) có hoành độ và tung độ bằng nhau.

Theo bài ra, cao độ của \({K_0}\) và \({K_1}\) lần lượt là 25 và 19 . Giả sử \({K_0}(x;y;25)\) và \({K_1}(x;y;19)\). Ta có \(MNPQ .{M_1}{N_1}{P_1}O\) là hình hộp chữ nhật nên \({K^\prime }K = OQ\), suy ra cao độ của \({K^\prime }\) bằng 30 . Do đó, \({K^\prime }(x;y;30)\).

Ta có \(\overrightarrow {{K^\prime }Q} = \overrightarrow {OQ} - \overrightarrow {O{K^\prime }} = 30\vec k - (x\vec i + y\vec j + 30\vec k) = - x\vec i - y\vec j \Rightarrow \overrightarrow {{K^\prime }Q} = ( - x; - y;0)\).

\(\begin{array}{l}\overrightarrow {NK'} = \overrightarrow {OK'} - \overrightarrow {ON} = (x\vec i + y\vec j + 30\vec k) - (90\vec i + 120\vec j + 30\vec k) = (x - 90)\vec i + (y - 120)\vec j\\ \Rightarrow \overrightarrow {NK'} = (x - 90;y - 120;0)\end{array}\)

Vi \({K^\prime }\) là giao hai đường chéo của hình chữ nhật M N P Q nên \({K^\prime }\) là trung điểm của N Q.

Suy ra \(\overrightarrow {{K^\prime }Q} = \overrightarrow {N{K^\prime }} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - x = x - 90}\\{ - y = y - 120}\\{0 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 45}\\{y = 60}\end{array}} \right.} \right.\).

Do vậy, \({K_0}(45;60;25);{K_1}(45;60;19)\) nên ta có

\(\overrightarrow {{K_0}{K_1}} = \overrightarrow {O{K_1}} - \overrightarrow {O{K_0}} = (45\vec i + 60\vec j + 19\vec k) - (45\vec i + 60\vec j + 25\vec k) = - 6\vec k \Rightarrow \overrightarrow {{K_0}{K_1}} = (0;0; - 6).\)

Do đó, \(a + b + c = - 6\).

Giải nhanh:

Từ giả thiết ta có \(\overrightarrow {{K_0}{K_1}} \) ngược hương với vec tơ đon vị trề trục \(0z{\rm{z}}\) là vec to \(\vec k = \) \((0;0;1)\) và do độ dà đoạn \({K_0}{K_1} = 6\) nên \(\overrightarrow {{K_0}{K_1}} = - 6\vec k = (0;0; - 6)\) nên ta có \(a + b + c = - 6\).

Đáp số : -6

Đáp án cần điền là: -6

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.