Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc ĐGNL/ĐGTD Tháng 12 ngày 13-14/12
 ↪ ĐGNL Hà Nội HSA (Trạm 2) ↪ ĐGNL HCM V-ACT (Trạm 2) ↪ ĐGTD Bách Khoa TSA (Trạm 4) ↪ ĐGNL SP Hà Nội SPT (Trạm 1)
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Hình vẽ trên mô tả mô hình một hệ thống leo núi trong nhà với

Câu hỏi số 743032:
Vận dụng


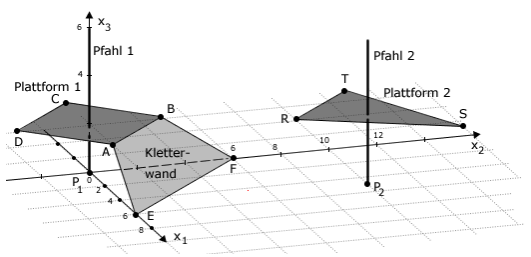
Hình vẽ trên mô tả mô hình một hệ thống leo núi trong nhà với các thành phần chính: hai sàn ngang (ABCD) và (RTS), mỗi sàn có một cột thẳng đứng \({P_1}\), \({P_2}\) và một tường leo AEFB gắn vào sàn ABCD.

Trong hệ tọa độ, mặt phẳng Oxy là mặt đất. Các sàn và vách leo được xem là các đa giác phẳng. Mỗi đơn vị chiều dài tương ứng với 1 mét thực tế. Các điểm cột trụ nhô lên khỏi mặt đất là \({P_1}(0;0;0)\)và \({P_2}(5;10;0)\). Biết các điểm \(A(3;0;2);B(0;3;2)\); \(E(6;0;0),F(0;6;0)\). Độ dày vật liệu của hệ thống không đáng kể. (Nguồn: https://www.abiturloesung.de; Abitur bayern 2018 Geometrie VI)

Đúng Sai
a) Phương trình mặt phẳng chứa bức tường leo là \(2x + 2y + 3z - 12 = 0\)
b) Bức tường leo và mặt đất tạo thành một góc 45 độ.
c) Một dây thừng được gắn ở trung điểm của cạnh trên của bức tường. Biết sợi dây dài hơn 20% so với khoảng cách giữa trung điểm cạnh trên và cạnh dưới của bức tường. Chiều dài của sợi dây thừng đó là 3m.
d) Một tấm lưới leo giúp người leo di chuyển từ sàn này ngang sang sàn ngang kia. Bốn đỉnh của lưới được cố định vào hai cột \({P_1},{P_2}\). Tại mỗi cột, khoảng cách giữa hai đỉnh lưới được cố định là 1,80m. Lưới được căng sao cho có thể xem nó là một tứ giác phẳng. Diện tích của tấm lưới là \(9\sqrt 5 \)\({m^2}\).

Đáp án đúng là: Đ; S; S; Đ

Quảng cáo

Xem lời giải
Câu hỏi:743032
Phương pháp giải

a) Viết phương trình mặt phẳng \(AEFB\) khi biết cặp vectơ chỉ phương.

b) Công thức xác định góc giữa hai mặt phẳng: \(\cos \alpha {\rm{\;}} = \dfrac{\vec n.\vec k}{\left| {\vec n} \right|.\left| {\vec k} \right|}\) với \(\vec n\), \(\vec k\) là hai vectơ pháp tuyến của hai mặt phẳng.

c) Xác định toạ độ trung điểm \(AB\) và \(EF\), tính khoảng cách giữa chúng sau đó suy ra độ dài dây thừng.

d) Tính \(P_1P_2\) là chiều dài tấm lưới, chiều rộng tấm lưới là 1,8 m. Tính diện tích tấm lưới.

Giải chi tiết

a) Đúng: Có \(\overrightarrow {AE} \left( {3;0; - 2} \right)\) và \(\overrightarrow {BF} \left( {0;3; - 2} \right)\) là cặp vectơ chỉ phương của mặt phẳng \((ABF)\).

Có \(\left[ {\overrightarrow {AE} ,\overrightarrow {BF} } \right] = \left( {6;6;9} \right)\)

Mặt phẳng chứa bức tường leo là \((AEFB)\) đi qua \(A(3;0;2)\)và nhận \(\vec n\left( {2;2;3} \right)\) làm vectơ pháp tuyến.

Phương trình mặt phẳng \((AEFB)\): \(2x + 2y + 3z - 12 = 0\).

b) Sai: Mặt đất có phương trình \(z = 0\) và có vectơ pháp tuyến là \(\vec k(0;0;1).\)

Gọi góc giữa hai mặt phẳng \((AEFB)\) và \((ABCD)\) là \(\alpha \), ta có

\(\begin{array}{*{20}{l}}{\cos \alpha {\rm{\;}} = \dfrac{{\vec n.\vec k}}{{\left| {\vec n} \right|.\left| {\vec k} \right|}} = \dfrac{{0 + 0 + 3}}{{\sqrt {{2^2} + {2^2} + {3^2}} .\sqrt {{1^2}} }} = \dfrac{3}{{\sqrt {17} }}}\\{ \Rightarrow \alpha {\rm{\;}} \approx 43,{3^o}.}\end{array}\)

c) Sai: Trung điểm của \(AB\) là \({M_1}\left( {\dfrac{3}{2};\dfrac{3}{2};2} \right)\);

Trung điểm EF là \({M_2}\left( {3;3;0} \right)\)

Có \({M_1}{M_2} = \left| {\overrightarrow {{M_1}{M_2}} } \right| = \sqrt {{{\left( {3 - \dfrac{3}{2}} \right)}^2} + {{\left( {3 - \dfrac{3}{2}} \right)}^2} + {{\left( {0 - 2} \right)}^2}}  = \dfrac{{\sqrt {34} }}{2}\)

Chiều dài sợ dây thừng là: \(\dfrac{{\sqrt {34} }}{2} + 0,2.\dfrac{{\sqrt {34} }}{2} \approx 3,5\)(m).

d) Đúng: Có \(\overrightarrow {{P_1}{P_2}} (5;10;0) \Rightarrow {P_1}{P_2} = \sqrt {{5^2} + {{10}^2} + {0^2}}  = 5\sqrt 5 .\)

Tấm lưới là hình chữ nhật với chiều dài \(5\sqrt 5 \)m và chiều rộng 1,8m.

Diện tích tấm lưới là \(1,8.5\sqrt 5  = 9\sqrt 5 \)\({m^2}.\)

Đáp án cần chọn là: Đ; S; S; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn