Một cửa hàng bán vở học sinh loại cao cấp với giá mỗi quyển là 50.000

Câu hỏi số 743049:

Vận dụng

Một cửa hàng bán vở học sinh loại cao cấp với giá mỗi quyển là 50.000 đồng. Với giá bán này, cửa hàng chỉ bán được khoảng 40 quyển. Cửa hàng dự định giảm giá bán, ước tính rằng nếu cửa hàng cứ giảm mỗi quyển 5.000 đồng thì số lượng vở bán được tăng thêm là 50 quyển. Xác định giá bán (đơn vị: nghìn đồng) để cửa hàng thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quyển vở là 30.000 đồng.

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:743049

Phương pháp giải

Gọi \(x\) là giá bán thực tế của mỗi quyển vở (\(30.000 \le x \le 50.000\)).

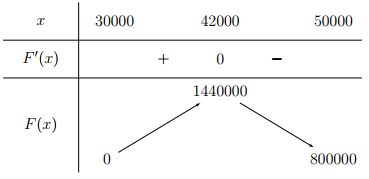
Dựa vào các dữ kiện của bài toán, xác định hàm lợi nhuận \(F(x)\) và khảo sát hàm số đó tìm giá trị lớn nhất.

Giải chi tiết

Gọi \(x\) là giá bán thực tế của mỗi quyển vở (\(30.000 \le x \le 50.000\)).

Giá 50000 đồng thì bán được 40 quyển.

Giảm giá 5000 đồng thì bán được thêm 50 quyển.

Giảm giá \(50000 - x\) thì bán được thêm được:

\(\dfrac{{50000 - x}}{{5000}}50 = (50000 - x)\dfrac{1}{{100}}\)

Do đó, số quyển vở bán được tương ứng với giá bán \(x\):

\(40 + (50000 - x)\dfrac{1}{{100}} = \dfrac{{ - 1}}{{100}}x + 540\)

Gọi \(F(x)\) là hàm lợi nhuận thu được \((F(x)\) : đồng).

Ta có:

\(\begin{array}{l}F(x) = \left( {\dfrac{{ - 1}}{{100}}x + 540} \right)(x - 30000)\\ = \dfrac{{ - 1}}{{100}}{x^2} + 840x - 16200000\end{array}\).

Bài toán trở thành tìm GTLN của

\(F(x) = \dfrac{{ - 1}}{{100}}{x^2} + 840x - 16200000\) với \(30000 \le x \le 50000\)

Ta có \({F^\prime }(x) = \dfrac{{ - 1}}{{50}}x + 840\).

Do đó, \({F^\prime }(x) = 0 \Leftrightarrow \dfrac{{ - 1}}{{50}}x + 840 = 0 \Leftrightarrow x = 42000\).

Bảng biến thiên:

Suy ra \(F(x)\) đạt GTLN tại \(x = 42000\).

Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi sách là 42 nghìn đồng.

Đáp án cần điền là: 42

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.