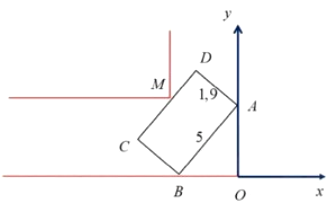
Thầy Trương muốn mua một chiếc ôtô. Ngõ từ đường vào sân nhà

Câu hỏi số 749643:

Thông hiểu

Thầy Trương muốn mua một chiếc ôtô. Ngõ từ đường vào sân nhà thầy hình chữ L.

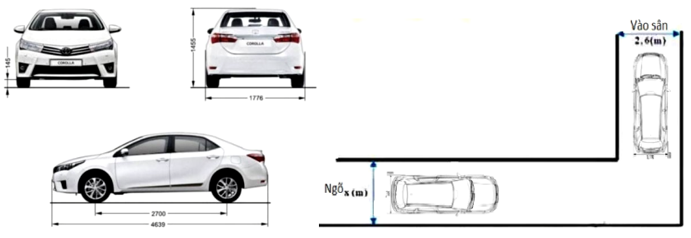
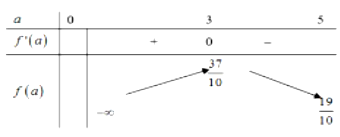
Đoạn đường đầu tiên có chiều rộng bằng \(x(\mathrm{~m})\), đoạn đường thẳng vào sân chiều rộng \(2,6(\mathrm{~m})\) Biết kích thước xe ôtô như hình vẽ trên (đơn vị milimet) và để ôtô đi qua an toàn thì chiều rộng và chiều dài tương ứng của đoạn đường phải lớn hơn kích thước thiết kế của ô tô một khoảng, cụ thể là \(5 m \times 1,9 m\) (chiều dài x chiều rộng). Để tính toán và thiết kế đường đi cho ôtô từ ngõ vào sân, thầy Trương coi ôtô như một khối hộp chữ nhật có kích thước chiều dài là \(5(\mathrm{~m})\), chiều rộng \(1,9(m)\). Chiều rộng nhỏ nhất của đoạn đường đầu tiên là \(x=\dfrac{p}{q}(m)\) (với \(p, q\) là các số nguyên dương và phân số \(\dfrac{p}{q}\) tối giản) để ôtô của thầy Trương có thể đi vào được sân (giả thiết ôtô không đi ra ngài đđoơng, không đi nghiêng và ôtô không bị biến dạng). Khi đó \(p+q\) bằng bao nhiêu?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:749643

Giải chi tiết

Chọn hệ trục \(O x y\) như hình vẽ. Khi đó, \(M(-2,6 ; h)\).

Gọi \(B(-a ; 0)\), suy ra \(A\left(0 ; \sqrt{25-a^2}\right), a>0\).

Từ đó, phương trình của \(A B\) là \(\dfrac{x}{-a}+\dfrac{y}{\sqrt{25-a^2}}=1\).

Do \(C D // A B\) nên phương trình \(C D\) là \(\dfrac{x}{-a}+\dfrac{y}{\sqrt{25-a^2}}-k=0\).

Khoảng cách giữa \(A B\) và \(C D\) là chiều rộng của ôtô và bằng \(1,9 \mathrm{~m}\) nên

\(\dfrac{|k-1|}{\sqrt{\left(\dfrac{1}{a}\right)^2+\left(\dfrac{1}{\sqrt{25-a^2}}\right)^2}}=1,9\)

\(\Leftrightarrow k=1+\dfrac{9,5}{a \sqrt{25-a^2}}\) vì \(C D\) nằm phía trên \(A B\) nên \(k>1\)

Phương trình \(C D\) được viết lại là

\(\dfrac{x}{-a}+\dfrac{y}{\sqrt{25-a^2}}-1-\dfrac{9,5}{a \sqrt{25-a^2}}=0\)

Điều kiện để ôtô đi qua được là \(M\) và \(O\) nằm khác phía đối với đường thẳng \(C D\).

Suy ra

\( \left(\dfrac{2,6}{a}+\dfrac{h}{\sqrt{25-a^2}}-1-\dfrac{9,5}{a \sqrt{25-a^2}}\right)\left(-1-\dfrac{9,5}{a \sqrt{25-a^2}}\right) \leq 0\)

\( \Leftrightarrow \dfrac{2,6}{a}+\dfrac{h}{\sqrt{25-a^2}}-1-\dfrac{9,5}{a \sqrt{25-a^2}} \geq 0 \)

\(\Leftrightarrow h \geq \sqrt{25-a^2}+\dfrac{9,5}{a}-\dfrac{2,6 \sqrt{25-a^2}}{a}\) (đúng với mọi \( a \in(0 ; 5].\)

Xét hàm số \(f(a)=\sqrt{25-a^2}+\dfrac{9,5}{a}-\dfrac{2,6 \sqrt{25-a^2}}{a}\) trên nửa khoảng \((0 ; 5]\).

Ta có \(f^{\prime}(a)=\dfrac{65-9,5 \sqrt{25-a^2}-a^3}{a^2 \sqrt{25-a^2}} \Rightarrow f^{\prime}(a)=0 \Leftrightarrow a=3 \in(0 ; 5)\).

Bảng biến thiên:

Do đó, \(h \geq f(a), \forall a \in(0 ; 5] \Leftrightarrow h \geq \dfrac{37}{10}\).

Vậy giá trị nhỏ nhất của x là \(x=\dfrac{37}{10}\)

Vậy \(p+q=47\) là giá trị cần tìm.

Đáp án cần điền là: 47

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.