Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280 kg chất \(A\) và 18 kg
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280 kg chất \(A\) và 18 kg chất \(B\). Với một tấn nguyên liệu loại \(I\), người ta có thể chiết xuất được 40 kg chất \(A\) và \(1,2{\rm{\;kg}}\) chất \(B\). Với một tấn nguyên liệu loại \(II\), người ta có thể chiết xuất được 20 kg chất \(A\) và 3 kg chất \(B\). Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
Đáp án đúng là: B
Quảng cáo
Gọi \(x\) và \(y\) lần lượt là số tấn nguyên liệu loại I và loại II mà người ta cần dùng.
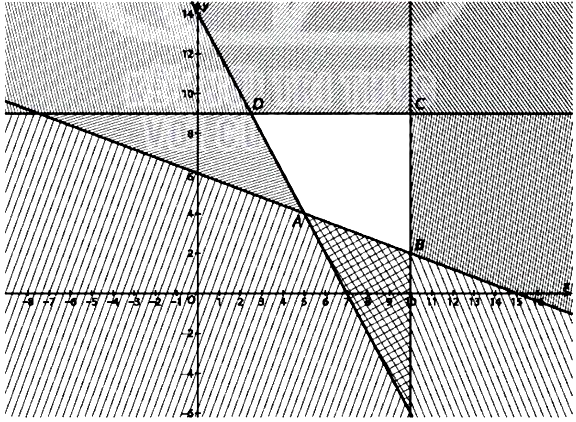
Từ giả thiết lập hệ bất phương trình, biểu diễn đồ thị miền nghiệm. khi đó GTLN đạt tại đỉnh đa giác miền nghiệm.
Gọi \(x\) và \(y\) lần lượt là số tấn nguyên liệu loại I và loại II mà người ta cần dùng.
Khi đó khối lượng chất \(A\) chiết xuất được là \(40x + 20y\left( {{\rm{\;kg}}} \right)\).
Khối lượng chất \(B\) chiết xuất được là \(1,2x + 3y\left( {{\rm{\;kg}}} \right)\).
Từ giả thiết ta có hệ bất phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{40x + 20y \ge 280}\\{1,2x + 3y \ge 18}\\{x \le 10}\\{y \le 9}\end{array}{\rm{\;}} \Leftrightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\{1,2x + 3y \ge 18}\\{x \le 10}\\{y \le 9}\end{array}} \right.} \right.\)
Hơn nữa, số tiền người ta phải trả đề mua nguyên liệu là \(F\left( {x;y} \right) = 4x + 3y\) (triệu đồng). Vậy bài toán trở thành tìm giá trị nhỏ nhất của \(F\left( {x;y} \right)\) với \(\left( {x;y} \right)\) thoả mãn hệ bất phương trình bậc nhất hai ần ở trên.
Bước 1. Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ần trên.
Miền nghiệm là miền tứ giác \(ABCD\) với \(A\left( {5;4} \right),B\left( {10;2} \right),C\left( {10;9} \right),D\left( {2,5;9} \right)\left( {{\rm{H}}.2.6} \right)\).
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
