Xét một chiếc bàn phẳng, có hai viên bi hình cầu được đặt trên mặt bàn. Gắn hệ trục tọa

Câu hỏi số 798790:

Vận dụng

Xét một chiếc bàn phẳng, có hai viên bi hình cầu được đặt trên mặt bàn. Gắn hệ trục tọa độ $O x y z$ sao cho mặt phẳng $(O x y)$ trùng với mặt bàn, trục $O z$ hướng thẳng đứng lên trên so với mặt bàn

và mỗi đơn vị trên các trục tương ứng với 1 cm . Ban đầu 2 viên bi này đứng yên trên mặt bàn, tâm của chúng lần lượt trùng với các điểm $I(-11 ; 5 ; 3)$ và $J(13 ;-2 ; 5)$.

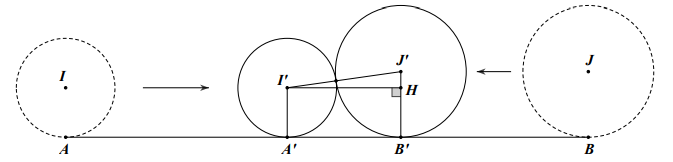
Tại một thời điểm, người ta đồng thời tác động cho 2 viên bi lăn về phía nhau trên mặt bàn theo cùng một đường thẳng với tốc độ không đổi là 5cm/s và 4cm/s (viên bi nhỏ hơn có tốc độ lớn hơn). Hỏi sau bao nhiêu giây kể từ khi tác động thì hai viên bi va chạm với nhau? (làm tròn kết quả đến hàng phần trăm).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:798790

Phương pháp giải

Giả sử viên bi 1 lăn đến A’, viên bi 2 lăn đến B’. Tính A’B’ dựa vào tam giác vuông

Giải chi tiết

Nhận xét: Bán kính viên bi chính là khoảng cách từ tâm đến mặt bàn, điểm tiếp xúc chính là hình chiếu vuông góc của tâm trên mặt bàn.

Viên bi thứ nhất có bán kính $r_1=3(\mathrm{~cm})$ và tiếp xúc với mặt bàn tại điểm $A(-11 ; 5 ; 0)$.

Viên bi thứ hai có bán kính $r_2=5(\mathrm{~cm})$ và tiếp xúc với mặt bàn tại điểm $B(13 ;-2 ; 0)$.

Vì 2 viên bi lăn thẳng về phía nhau trên mặt bàn nên điểm tiếp xúc của 2 viên bi với mặt bàn luôn chạy trên đoạn thẳng $A B$.

Giâ sử tại thời điểm $t$ giây thì hai viên bi va chạm với nhau.

Khi đó viên bi thứ nhất di chuyển được quãng đường $A A^{\prime}=5 t(\mathrm{~cm})$, viên bi thứ 2 di chuyển được quãng đường $B B^{\prime}=4 t(\mathrm{~cm})$.

Ta có $A^{\prime} B^{\prime}=I^{\prime} H=\sqrt{I^{\prime} J^{\prime 2}-J^{\prime} H^2}=\sqrt{\left(r_1+r_2\right)^2-\left(r_2-r_1\right)^2}=2 \sqrt{15}$.

Mà $A B=\sqrt{24^2+7^2}=25 \Rightarrow A A^{\prime}+B B^{\prime}=25-2 \sqrt{15}$.

Do đó $5 t+4 t=25-2 \sqrt{15} \Rightarrow t=\dfrac{25-2 \sqrt{15}}{9} \approx 1,92$ giây.

Vậy sau khoảng 1,92 giây thì hai viên bi va chạm.

Đáp án cần điền là: 1,92

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.