Gọi $H$ là trực tâm của tam giác $ABC$. Phương trình các cạnh và
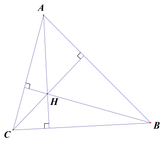
Gọi $H$ là trực tâm của tam giác $ABC$. Phương trình các cạnh và đường cao của tam giác là $AB$: $7x - y + 4 = 0$; $BH$: $2x + y - 4 = 0$; $AH$: $x - y - 2 = 0$. Phương trình đường cao $CH$ của tam giác $ABC$ là
Đáp án đúng là: A
Quảng cáo
Công thức:
- Phương trình đường thẳng đi qua điểm $M(x_{0};y_{0})$ với vector pháp tuyến $\overset{\rightarrow}{n} = (A;B)$ là:
$A(x - x_{0}) + B(y - y_{0}) = 0$
1. Tìm tọa độ trục tâm H bằng cách giải hệ phương trình của hai đường cao đã cho (AH và BH).
2. Xác định vector chỉ phương $u_{AB}$ của cạnh AB.
3. Do đường cao CH vuông góc với AB, vector pháp tuyến của CH chính là $u_{AB}$.
4. Viết phương trình đường thẳng CH đi qua H và có vector pháp tuyến vừa tìm được.
Gọi $H\left( {x;y} \right)$.
Ta có $H = AH \cap BH$.
Nên tọa độ điểm $H$ là nghiệm của hệ phương trình: $\left\{ \begin{array}{l} {2x + y = 4} \\ {x - y = 2} \end{array} \right.$$\left. \Leftrightarrow\left\{ \begin{array}{l} {x = 2} \\ {y = 0} \end{array} \right. \right.$, suy ra $H\left( {2;0} \right)$.
Đường thẳng $AB$ có vectơ chỉ phương là $\overset{\rightarrow}{u} = \left( {1;7} \right)$.
Đường cao $CH$ vuông góc với cạnh $AB$ nên nhận $\overset{\rightarrow}{u}$ làm vectơ pháp tuyến.
Vậy phương trình tổng quát của đường cao $CH$ là $\left( {x - 2} \right) + 7\left( {y - 0} \right) = 0$$\left. \Leftrightarrow x + 7y - 2 = 0 \right.$.
Đáp án cần chọn là: A
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
