Cho hình vẽ sau. Kiểm tra tính đúng sai của các khẳng định
Cho hình vẽ sau. Kiểm tra tính đúng sai của các khẳng định sau
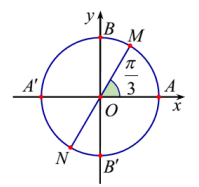
| Đúng | Sai | |
|---|---|---|
| a) Số đo góc lượng giác $(OM,OA)$ là $\text{sd}(\text{OM},\text{OA}) = \dfrac{\pi}{3} + \text{k}2\pi(\text{k} \in {\mathbb{Z}})$. | ||
| b) $\text{sd}(\text{ON},\text{OA}) = \text{sd}(\text{ON},\text{OM}) - \text{sd}(\text{OA},\text{OM})$. | ||
| c) Độ dài cung tròn AM lớn là: $l_{AM} = \dfrac{2\pi}{3}$. | ||
| d) Hai điểm M, N biểu diễn các cung có số đo là: $x = \dfrac{\pi}{3} + k\pi(k \in {\mathbb{Z}})$. |
Đáp án đúng là: S; Đ; S; Đ
Quảng cáo
Áp dụng các công thức cơ bản
Công thức tổng quát của sổ đo cung: Số đo cung lượng giác của một điểm $M$ là $x_{0} + k2\pi(k \in {\mathbb{Z}})$, trong đó $x_{0}$ là một giá trị cụ thể của số đo cung đó.
Hệ thức Chasles: ${sd}(OA,OC) = sd(OA,OB) + sd(OB,OC)$. Công thức này cho phép cộng hoặc trừ số đo các cung.
Số đo góc lượng giác: ${sd}(OM,OA) = - {sd}(OA,OM)$.
Độ dài cung tròn: $l = R \cdot \alpha$, với $R$ là bán kính đường tròn và $\alpha$ là số đo cung (radian). Đối với đường tròn lượng giác, $R = 1$, nên $l = \alpha$.
Đối xứng tâm: Nếu điểm $N$ đối xứng với $M$ qua tâm $O$, thi ${sd}(ON,OM) = \pi$. Do đó, ${sd}(OA,ON) = {sd}(OA,OM) + \pi$.
Đáp án cần chọn là: S; Đ; S; Đ
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
