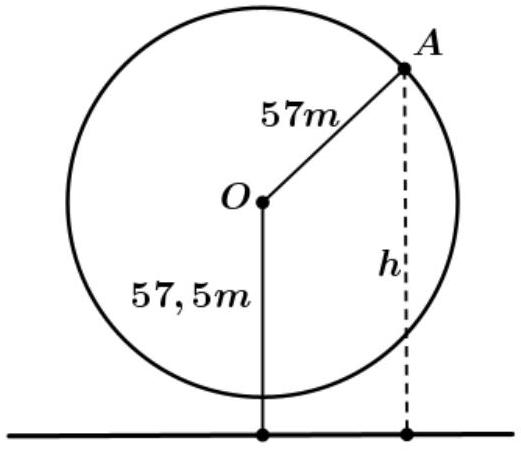
Một vòng quay trò chơi có bán kính 57 m , trục quay cách mặt đất $57,5\text{~m}$, quay đều mỗi

Câu hỏi số 817909:

Vận dụng

Một vòng quay trò chơi có bán kính 57 m , trục quay cách mặt đất $57,5\text{~m}$, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách $h\left( \text{~m} \right)$ từ một cabin gắn tại điểm $A$ của vòng quay đến mặt đất được tính bởi công thức: $h(t) = 57\text{sin}\left( {\dfrac{2\pi}{15}t - \dfrac{\pi}{2}} \right) + 57,5$ với $t$ là thời gian quay của vòng quay tính bằng phút $\left( {t \geq 0} \right)$. Khi quay một vòng lần thứ nhất tính từ thời điểm $t = 0$ (phút), tại thời điểm nào của $t$ thì cabin ở vị trí cao nhất?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:817909

Phương pháp giải

Giải phương trình $\text{sin}\left( {\dfrac{2\pi}{15}t - \dfrac{\pi}{2}} \right) = 1$ tìm t với $t \in \left\lbrack {0;15} \right\rbrack$

Công thức cơ bản: $\left. \sin x = \sin a\Leftrightarrow\left\lbrack \begin{array}{l} {x = a + k2\pi} \\ {x = \pi - a + k2\pi} \end{array} \right. \right.$

Giải chi tiết

Khi quay một vòng, cabin ở vị trí cao nhất khi $\text{sin}\left( {\dfrac{2\pi}{15}t - \dfrac{\pi}{2}} \right) = 1$

$\left. \dfrac{2\pi}{15}t - \dfrac{\pi}{2} = \dfrac{\pi}{2} + k2\pi\Leftrightarrow\dfrac{2\pi}{15}t = \pi + k2\pi\Leftrightarrow t = \dfrac{15}{2} + 15k \right.$

Vì $\left. t \in \left\lbrack {0;15} \right\rbrack\Rightarrow 0 \leq \dfrac{15}{2} + 15k \leq 15\Rightarrow k = 0\Rightarrow t = \dfrac{15}{2} \right.$ hay $t = 7,5$ (phút)

Đáp án cần điền là: 7,5

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.