Một cây cầu có dạng cung $OA$ của đồ thị hàm số $y = 4,8\text{sin}\dfrac{x}{9}$ và được mô tả

Câu hỏi số 817913:

Vận dụng

Một cây cầu có dạng cung $OA$ của đồ thị hàm số $y = 4,8\text{sin}\dfrac{x}{9}$ và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở hình dưới đây:

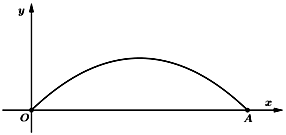
Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao $3,6m$ so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Tính chiều rộng tối đa của khối hàng hóa đó để sà lan có thể đi qua được gầm cầu.

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:817913

Phương pháp giải

Giải phương trình $y = 0$ tìm giao điểm của hàm số với Ox tính khoảng cách OA.

Tìm hoành độ giao điểm của $y = 3,6$ với $y = 4,8\text{sin}\dfrac{x}{9}$ tìm $x_{1};x_{2}$

Chiều rộng của khối hàng hoá bằng $d = \left| {x_{1} - x_{2}} \right|$

Giải chi tiết

Giải phương trình $\left. y = 0\Leftrightarrow 4,8\text{sin}\dfrac{x}{9} = 0\Leftrightarrow\text{sin}\dfrac{x}{9} = 0\Leftrightarrow\dfrac{x}{9} = k\pi\Leftrightarrow x = k9\pi\left( {k \in {\mathbb{Z}}} \right) \right.$.

Do đó đồ thị cắt trục $Ox$ tại các điểm có hoành độ $0;9\pi;18\pi;\ldots$.

Vì thế $A\left( {9\pi;0} \right)$ nên chiều rộng của con sông là $OA = 9\pi \approx 28,3m$

Xét đường thẳng $y = 3,6$

Ta có $y = 4,8\text{sin}\dfrac{x}{9} \leq 4,8$, nên đường thẳng $y = 3,6$ cắt một phần đồ thị của hàm số $y = 4,8\text{sin}\dfrac{x}{9}$ tại hai điểm $M\left( {x_{1};3,6} \right),N\left( {x_{2};36} \right)$.

Giải phương trình $\left. 4,8\text{sin}\dfrac{x}{9} = 3,6\Leftrightarrow\text{sin}\dfrac{x}{9} = \dfrac{3}{4}(1),x_{1},x_{2} \right.$ là hai nghiệm dương nhỏ nhất của (1) $- 1 \leq \dfrac{3}{4} \leq 1$ nên tồn tại một số $\alpha \in \left\lbrack {- \dfrac{\pi}{2};\dfrac{\pi}{2}} \right\rbrack$ sao cho $\text{sin}\alpha = \dfrac{3}{4}$.

Ta có $\left. \text{sin}\dfrac{x}{9} = \text{sin}\alpha\Leftrightarrow\left\lbrack \begin{array}{l} {\dfrac{x}{9} = \alpha + k2\pi} \\ {\dfrac{x}{9} = \pi - \alpha + k2\pi} \end{array}\Leftrightarrow\left\lbrack \begin{array}{l} {x = 9\alpha + k18\pi} \\ {x = 9\pi - 9\alpha + k18\pi} \end{array} \right. \right. \right.$

Do $x_{1};x_{2} \in \left( {0;9\pi} \right)$ nên $x_{1} \approx 9\alpha \approx 7,6325;x_{1} \approx 9\pi - 9\alpha \approx 20,6418$ nên $x_{2} - x_{1} < 13,1$.

Vậy chiều rộng của khối hàng hoá tối đa là $13m$

Đáp án cần điền là: 13

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.