Để đo chiều cao của một cây lớn, một bạn từ vị trí $H$ trên ban công của một toà nhà, có

Câu hỏi số 819482:

Vận dụng

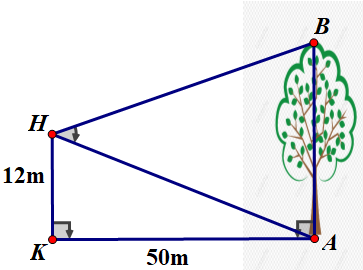
Để đo chiều cao của một cây lớn, một bạn từ vị trí $H$ trên ban công của một toà nhà, có độ cao so với mặt đất $12m$, bạn đó dùng dụng cụ đo góc quan sát được cây $AB$dưới góc $\widehat{AHB} = 50{^\circ}$. Biết khoảng cách từ chân tường nhà đến gốc cây là $KA = 50m$, tính chiều cao của cây (làm tròn đến hàng đơn vị).

A diagram of a triangle with a tree and text

Description automatically generated

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:819482

Phương pháp giải

Sử dụng hệ thức $\tan A = \dfrac{HK}{AK}$ trong tam giác AHK để tính góc HAK, HAB, từ đó tính góc HBA.

Dùng định lí Pythagoras trong tam giác AHK tính AH.

Áp dụng định lí sin trong tam giác AHB để tính AB: $\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}$.

Giải chi tiết

$\begin{array}{l} {\tan\widehat{HAK} = \dfrac{12}{50} = \dfrac{6}{25}} \\ \left. \Rightarrow\widehat{HAK} \approx 13,5^{0}\Rightarrow\widehat{HAB} \approx 76,5^{0} \right. \\ \left. \Rightarrow\widehat{HBA} \approx 180^{0} - \left( {50^{0} + 76,5^{0}} \right) \approx 53,5^{0} \right. \end{array}$

Lại có: $AH = \sqrt{HK^{2} + AK^{2}} = \sqrt{12^{2} + 50^{2}} = 2\sqrt{661}$.

Áp dụng định lý sin trong tam giác $AHB$ ta có:

$\begin{array}{l} \left. \dfrac{AB}{\sin\widehat{AHB}} = \dfrac{AH}{\sin\widehat{ABH}}\Leftrightarrow\dfrac{AB}{\sin 50^{0}} = \dfrac{AH}{\sin 53,5^{0}} \right. \\ \left. \Rightarrow AB = \dfrac{\sin 50^{0}}{\sin 53,5^{0}}.AH \right. \\ {\ \ \ \ \ \ \ \ \ = \dfrac{\sin 50^{0}}{\sin 53,5^{0}}.2\sqrt{661}} \\ {\ \ \ \ \ \ \ \ \ \approx 49\,(m)} \end{array}$

Đáp án cần điền là: 49

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10