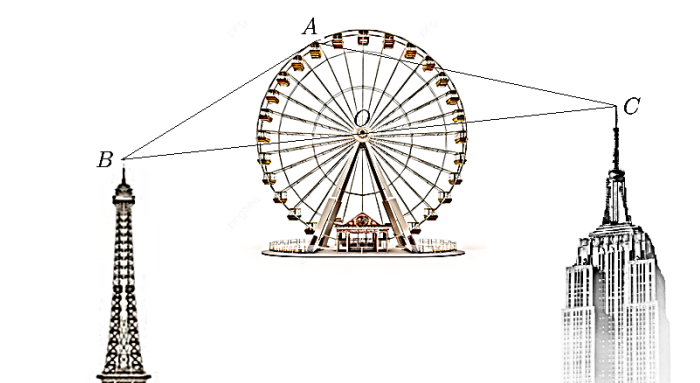
Một người ngồi trên đu quay có đường kính 115 m, quan sát hai đỉnh tháp $B,\, C$ cách nhau một

Câu hỏi số 819486:

Vận dụng

Một người ngồi trên đu quay có đường kính 115 m, quan sát hai đỉnh tháp $B,\, C$ cách nhau một khoảng $BC = 345$ m (minh họa như hình dưới). Biết rằng tâm $O$ của đu quay là trung điểm của đoạn thẳng $BC$. Tính khoảng cách từ vị trí người ngồi trên đu quay đến đỉnh tháp $B$ khi góc quan sát từ vị trí người đó đến hai đỉnh tháp (góc $\widehat{BAC}$) là nhỏ nhất (kết quả làm tròn đến hàng đơn vị)

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:819486

Phương pháp giải

Áp dụng định lý côsin trong $\bigtriangleup OAB$ và $\bigtriangleup OAC$ :

$AB = \sqrt{OA^{2} + OB^{2} - 2OA.OB\cos\alpha},\quad AC = \sqrt{OA^{2} + OC^{2} + 2OA.OC\cos\alpha}$

Dùng định lí cos cho $\angle BAC$: $\cos\angle BAC = \dfrac{AB^{2} + AC^{2} - BC^{2}}{2AB \cdot AC}$

Muốn $\angle BAC$ nhỏ nhất ta cần $\cos\angle BAC$ lớn nhất, tính $\alpha$.

Thay giá trị $\alpha$ trở lại công thức $AB = \sqrt{OA^{2} + OB^{2} - 2OA.OB\cos\alpha}$ để tính khoảng cách AB.

Giải chi tiết

Có $OB = OC = 172,5$ m, $OA = 57,5$ m. Suy ra $OB = OC = 3OA$.

Đặt $OA = a$ và $\widehat{AOB} = \alpha$. Ta có $OB = OC = 3a,\ BC = 6a$.

Áp dụng định lý côsin trong các tam giác $OAB$ và $OAC$, ta có

$AB = \sqrt{a^{2} + 9a^{2} - 2.a.3a.\cos\alpha} = a\sqrt{10 - 6\cos\alpha}$;

$AC = \sqrt{a^{2} + 9a^{2} - 2.a.3a.\cos(180{^\circ} - \alpha)} = a\sqrt{10 + 6\cos\alpha}.$

Từ đó $\cos\widehat{BAC} = \dfrac{10 - 6\cos\alpha + 10 + 6\cos\alpha - 36}{2\sqrt{\left( {10 - 6\cos\alpha} \right)\left( {10 + 6\cos\alpha} \right)}} = \dfrac{- 8}{\sqrt{100 - 36\cos^{2}\alpha}}$.

Do $\cos^{2}\alpha \geq 0$ nên $\sqrt{100 - 36\cos^{2}\alpha} \leq 10$, suy ra $\cos\widehat{BAC} \leq \dfrac{- 8}{10} = \dfrac{- 4}{5}$.

Khi đó $\widehat{BAC} \geq 143,13{^\circ}$. Vậy góc quan sát nhỏ nhất là $143,13{^\circ}$.

Khi đó $AB = a\sqrt{10} \approx 182$ m.

Đáp án cần điền là: 182

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10