Bạn An đang nằm nghe nhạc trong phòng hình hộp chữ nhật, sàn nhà là

Câu hỏi số 823743:

Vận dụng

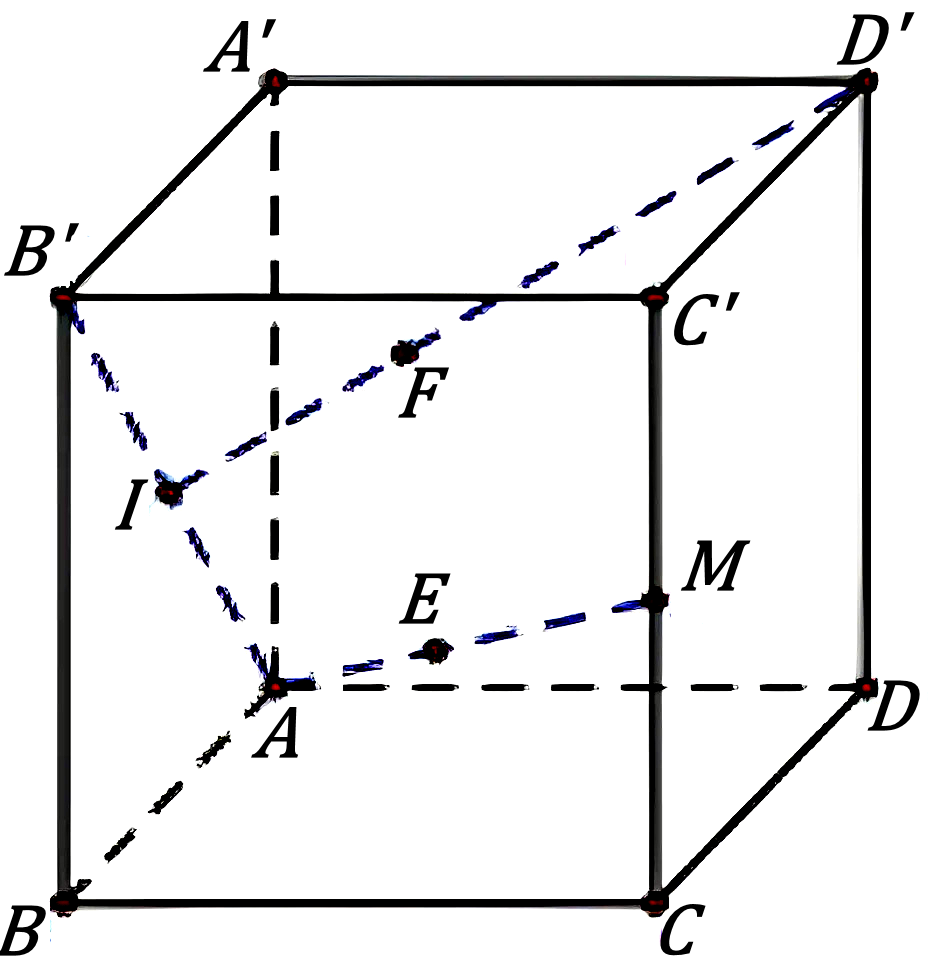
Bạn An đang nằm nghe nhạc trong phòng hình hộp chữ nhật, sàn nhà là hình vuông cạnh bằng 4 m, chiều cao của phòng là 3,2 m và phát hiện ra hai con nhện đang chăng tơ trong căn phòng của An, hai con nhện luôn di chuyển trên hai đường thẳng khác nhau. Giả sử căn phòng được mô hình hóa là hình hộp chữ nhật $ABCD \cdot A'B'C'D'$ với $ABCD$ là nền phòng của An thì con nhện thứ nhất được coi như điểm $E$ di chuyển trên đường dây tơ nối từ đỉnh $A$ đến trung điểm $M$ của $CC'$, còn con nhện thứ hai được coi như điểm $F$ di chuyển trên đường dây tơ nối từ $D'$ đến tâm $I$ của mặt bên $ABB'A'$. Tính khoảng cách giữa hai con nhện khi đường thẳng đi qua hai con nhện vuông góc với trần nhà (đơn vị mét, kết quả làm tròn đến hàng phần chục).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:823743

Phương pháp giải

Gắn hệ trục tọa độ Oxyz và sử dụng hình học giải tích trong không gian.

Gắn hệ trục tọa độ và xác định tọa độ các đỉnh, điểm M và tâm I.

Tham số hóa tọa độ hai con nhện E và F trên hai đường chăng tơ AM và D′I.

Sử dụng điều kiện vuông góc: Đường thẳng EF vuông góc với trần nhà (A′B′C′D′) ⇔EF cùng phương với vectơ pháp tuyến của trần nhà (ví dụ AA′).

Giải hệ phương trình để tìm tham số và tính EF

Giải chi tiết

Gắn hệ trục $Oxyz$ sao cho $A \equiv O;AB \equiv Ox;AD \equiv Oy;AA' \equiv Oz$.

Ta có $A\left( {0;0;0} \right);A'\left( {0;0;3,2} \right);M\left( {4;4;1,6} \right);D'\left( {0;4;3,2} \right);I\left( {2;0;1,6} \right)$.

Gọi $E\left( {x,y,z} \right),F\left( {m,n,p} \right)$.

Giả sử $\left. \overset{\rightarrow}{AE} = a\overset{\rightarrow}{AM}\Leftrightarrow\left\{ \begin{array}{l} {x = 4a} \\ {y = 4a} \\ {z = 1,6a} \end{array}\Rightarrow E\left( {4a;4a;1,6a} \right) \right. \right.$

+) $\left. \overset{\rightarrow}{D^{\prime}F} = b\overset{\rightarrow}{D^{\prime}I}\Leftrightarrow\left\{ \begin{array}{l} {m = 2b} \\ {n - 4 = - 4b} \\ {p - 3,2 = - 1,6b} \end{array}\Leftrightarrow\left\{ \begin{array}{l} {m = 2b} \\ {n = 4 - 4b} \\ {p = 3,2 - 1,6b} \end{array}\Rightarrow F\left( {2b;4 - 4b;3,2 - 1,6\text{b}} \right) \right. \right. \right.$

Ta có $\overset{\rightarrow}{EF} = \left( {2b - 4a;4 - 4b - 4a;3,2 - 1,6b - 1,6a} \right);\overset{\rightarrow}{AA^{\prime}} = \left( {0;0;3,2} \right)$

Để đường thẳng đi qua hai con nhện vuông góc với trần nhà thì $\overset{\rightarrow}{EF}$ cùng phương với $\overset{\rightarrow}{AA^{\prime}}$

Nên $\left\{ \begin{array}{l} {2b - 4a = 0} \\ {4 - 4b - 4a = 0} \end{array}\Leftrightarrow\left\{ \begin{array}{l} {a = \dfrac{1}{3}} \\ {b = \dfrac{2}{3}} \end{array} \right. \right.$. Khi đó $\left. \overset{\rightarrow}{EF} = \left( {0;0;1,6} \right)\Rightarrow EF = 1,6 \right.$.

Vậy khoảng cách giữa hai con nhện bằng 1,6 m.

Đáp án cần điền là: 1,6

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.