Trong công viên, có một hồ nước hình bán nguyệt (một nửa đường tròn) đường kính $AB =
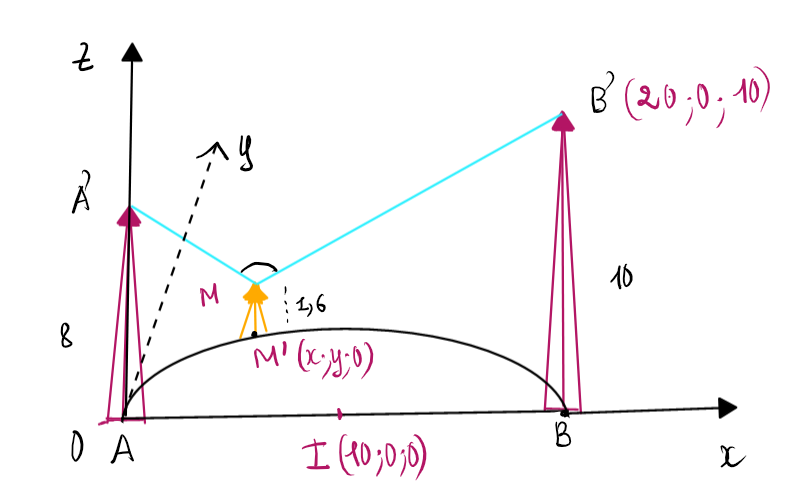
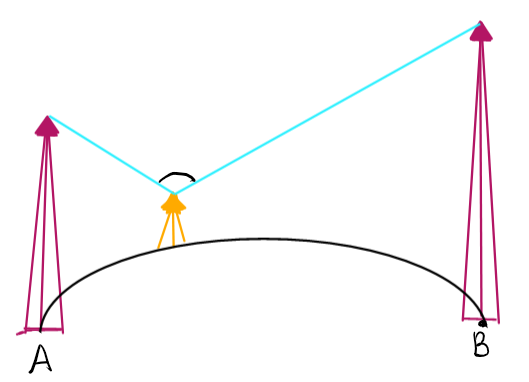
Trong công viên, có một hồ nước hình bán nguyệt (một nửa đường tròn) đường kính $AB = 20\text{m}\text{.}$Tại $A$và $B$người ta dựng hai bức tượng cao lần lượt là $8\text{m}$và $10\text{m}\text{.}$ Một người đứng trên phần cung tròn của bờ hồ muốn đặt máy ảnh cao $1,6\text{m}$để chụp toàn cảnh hai bức tượng. Gọi góc quan sát $\alpha$ là góc tạo bởi hai tia nối vị trí đặt máy ảnh với hai đỉnh của các bức tượng. Khi người đó di chuyển trên phần cung tròn của bờ hồ thì góc quan sát lớn nhất bằng ________ độ. (làm tròn hàng đơn vị)
Đáp án đúng là: 78
Quảng cáo
Gắn hệ trục toạ độ Oxy với A là gốc toạ độ từ đó tính góc giữa hai đường thẳng
$\cos BAC = \dfrac{BA^{2} + AC^{2} - BC^{2}}{2BA.AC}$
Gọi điểm $M'\left( {x;y,0} \right) \in \left( {I\left( {10;0} \right),R = 10} \right):\left( {x - 10} \right)^{2} + y^{2} = 10^{2}$
$\begin{array}{l} {A'\left( {0;0;8} \right),B'\left( {20;0;10} \right),M\left( {x;y;1,6} \right)} \\ \left. \Rightarrow\left\{ \begin{array}{l} {MA'^{2} = x^{2} + y^{2} + 6,4^{2} = 20x + 40,96} \\ {MB'^{2} = \left( {x - 20} \right)^{2} + y^{2} + 8,4^{2} = 470,56 - 20x} \end{array} \right. \right. \end{array}$
$\begin{array}{l} {\cos\alpha = \dfrac{MA'^{2} + MB'^{2} - B'A'^{2}}{2MA'.MB'} = \dfrac{107,52}{2\sqrt{\left( {20x + 40,96} \right).\left( {470,56 - 20x} \right)}}} \\ \left. \cos\alpha_{\min} = \dfrac{672}{3197}\Leftrightarrow x = 10,74\Rightarrow\alpha_{\max} \approx 78^{o} \right. \end{array}$
Đáp án cần điền là: 78
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
