Cho đường tròn tâm \(\left( O;R \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm
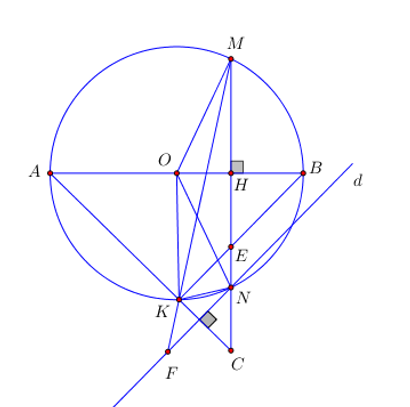
Cho đường tròn tâm \(\left( O;R \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn \(\left( O;R \right)\) sao cho đoạn thẳng AC cắt đường tròn \(\left( O;R \right)\) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
b) Chứng minh CA.CK = CE.CH
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
d) Khi KE = KC. Chứng minh OK // MN.
Quảng cáo
a) Chứng minh tứ giác AHEK có tổng hai góc đối bằng 1800.
b) Chứng minh tam giác CKE đồng dạng với tam giác CHA.
c) Chứng minh hai góc ở đáy của tam giác NFK bằng nhau.
d) Chứng minh tam giác OBK vuông cân tại O \(\Rightarrow OK\bot OB\), từ đó suy ra OK // MN.
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
Ta có \(\widehat{AKB}={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow \widehat{AKE}={{90}^{0}}\)
Xét tứ giác AHEK có \(\widehat{AKE}+\widehat{AHE}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow \) tứ giác AHEK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh CA.CK = CE.CH
Xét tam giác CKE và tam giác CHA có:
\(\widehat{CKE}=\widehat{CHA}={{90}^{0}};\)
\(\widehat{ACH}\) chung;
\(\Rightarrow \Delta CKE\backsim \Delta CHA\,\,\left( g.g \right)\Rightarrow \frac{CK}{CH}=\frac{CE}{CA}\Rightarrow CA.CK=CE.CH\)(đpcm).
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
Ta có \(d\bot AC;\,\,\widehat{AKB}={{90}^{0}}\Rightarrow BK\bot AK\Rightarrow BK\bot AC\Rightarrow d//BK\). (từ vuông góc đến song song).
Xét tam giác OMN có \(OM=ON\left( =R \right)\Rightarrow \Delta OMN\) cân tại O.
\(\Rightarrow \) Đường cao OH đồng thời là đường phân giác \(\Rightarrow \widehat{MOB}=\widehat{NOB}\Rightarrow \) sđ cung MB = sđ cung NB.
\(\Rightarrow \widehat{MKB}=\widehat{NKB}\) (hai góc nội tiếp chắn hai cung bằng nhau).
Ta có \(\widehat{KFN}=\widehat{MKB}\) (đồng vị);
\(\widehat{KNF}=\widehat{NKB}\) (so le trong);
Mà \(\widehat{MKB}=\widehat{NKB}\,\,\left( cmt \right)\Rightarrow \widehat{KFN}=\widehat{KNF}\Rightarrow \Delta NEK\) cân tại K.
d) Khi KE = KC. Chứng minh OK // MN.
Ta có \(\widehat{AKB}={{90}^{0}}\Rightarrow BK\bot AK\Rightarrow BK\bot AC\Rightarrow \Delta KEC\) vuông tại K.
Lại có KE = KC (gt) \(\Rightarrow \Delta KEC\) vuông cân tại K \(\Rightarrow \widehat{KEC}={{45}^{0}}\) ;
\(\Rightarrow \widehat{HEB}=\widehat{KEC}={{45}^{0}}\) (đối đỉnh) \(\Rightarrow \Delta HEB\) vuông cân tại H \(\Rightarrow \widehat{HBE}={{45}^{0}}\Rightarrow \widehat{OBK}={{45}^{0}}\)
Tam giác OBK có \(OB=OK\ \left( =R \right)\Rightarrow \Delta OBK\) cân tại O \(\Rightarrow \widehat{OBK}=\widehat{OKB}={{45}^{0}}\)
\(\Rightarrow \widehat{BOK}={{180}^{0}}-{{45}^{0}}-{{45}^{0}}={{90}^{0}}\Rightarrow \Delta BOK\) vuông cân tại \(O\Rightarrow OK\bot OB\) ;
Lại có \(MN\bot AB\,\,\left( gt \right)\Rightarrow MN\bot OB\).
Vậy MN // OK.
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
