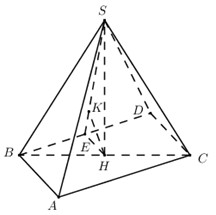
Cho hình chóp S.ABC có đáy ABC vuông cân tại A, \(AB = a\sqrt 2 \); tam giác SBC đều nằm trong mặt
Cho hình chóp S.ABC có đáy ABC vuông cân tại A, \(AB = a\sqrt 2 \); tam giác SBC đều nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách giữa hai đường thẳng AC và SB ta được kết quả là:
Đáp án đúng là: B
Quảng cáo
+) Dựng hình bình hành \(ABDC\). Chứng minh \(d\left( {SB;AC} \right) = d\left( {C;\left( {SBD} \right)} \right)\).
+) Sử dụng phương pháp đổi điểm tính khoảng cách.
Gọi \(H\) là trung điểm của \(BC \Rightarrow SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)\).
Dựng hình bình hành \(ABDC\) ta có \(BD//AC \Rightarrow AC//\left( {SBD} \right) \Rightarrow d\left( {SB;AC} \right) = d\left( {AC;\left( {SBD} \right)} \right) = d\left( {C;\left( {SBD} \right)} \right)\).
Ta có
\(\begin{array}{l}CH \cap \left( {SBD} \right) = B \Rightarrow \dfrac{{d\left( {C;\left( {SBD} \right)} \right)}}{{d\left( {H;\left( {SBD} \right)} \right)}} = \dfrac{{CB}}{{HC}} = 2\\ \Rightarrow d\left( {C;\left( {SBD} \right)} \right) = 2d\left( {H;\left( {SBD} \right)} \right)\end{array}\).
Gọi E là trung điểm của \(BD\) ta có \(EH\) là đường trung bình của tam giác \(BCD\).
\( \Rightarrow EH//CD//AB \Rightarrow EH \bot AC \Rightarrow EH \bot BD\).
Ta có \(\left\{ \begin{array}{l}BD \bot EH\\BD \bot SH\end{array} \right. \Rightarrow BD \bot \left( {SEH} \right)\).
Trong \(\left( {SEH} \right)\) kẻ \(HK \bot SE\) ta có \(\left\{ \begin{array}{l}HK \bot SE\\HK \bot BD\end{array} \right. \Rightarrow HK \bot \left( {SBD} \right) \Rightarrow d\left( {H;\left( {SBD} \right)} \right) = HK\).
Ta có \(EH = \dfrac{1}{2}CD = \dfrac{1}{2}AB = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác vuông \(ABC\) có \(BC = a\sqrt 2 .\sqrt 2 = 2a \Rightarrow \Delta SBC\) đều cạnh \(2a\).
\( \Rightarrow SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác vuông \(SHE\) ta có : \(HK = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {3{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{a\sqrt {21} }}{7}\).
Vậy \(d\left( {SB;AC} \right) = 2HK = \dfrac{{2a\sqrt {21} }}{7}\).
Chọn B.
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
