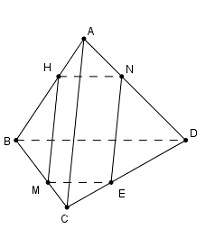
Cho tứ diện \(ABCD\) có \(BC = 9,AC = 6\) và \(BD = 3\) (tham khảo hình vẽ). Điểm \(M\) di chuyển trên
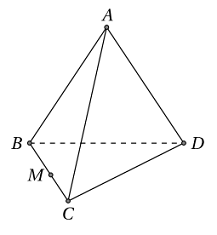
Cho tứ diện \(ABCD\) có \(BC = 9,AC = 6\) và \(BD = 3\) (tham khảo hình vẽ). Điểm \(M\) di chuyển trên cạnh \(BC.\) Mặt phẳng \(\left( \alpha \right)\) qua \(M,\) song song với \(AC\) và \(BD\) cắt tứ diện theo thiết diện là một tứ giác. Khi \(M\) di chuyển đến vị trí \({M_0}\) để thiết diện đó là một hình thoi, hãy tính tích \({M_0}B.{M_0}C.\)
Đáp án đúng là: C
Quảng cáo
+ Dựng mặt phẳng \(\left( \alpha \right)\) theo mối quan hệ song song với \(AC,BD\)
+ Tìm thiết diện của mặt phẳng \(\left( \alpha \right)\) với hình chóp
+ Dựa vào điều kiện hình thoi và định lý Ta-lét để tính toán.
Trong \(\left( {ABC} \right)\) kẻ \(MH//AC\left( {H \in AB} \right)\)
Trong \(\left( {BCD} \right)\) kẻ \(ME//DB\left( {E \in DC} \right)\)
Trong \(\left( {ABD} \right)\) kẻ \(HN//AD\left( {N \in AD} \right)\)
Suy ra \(HN//ME\).
Theo định lý Ta-lét ta có : \(\dfrac{{HN}}{{BD}} = \dfrac{{AH}}{{AB}} = \dfrac{{MC}}{{BC}} = \dfrac{{ME}}{{BD}} \Rightarrow HN = ME\)
Từ đó \(MENH\) là hình bình hành.
Ta có \(\left( \alpha \right) \equiv \left( {MENH} \right)\) và \(\left\{ \begin{array}{l}\left( {MENH} \right) \cap \left( {ABC} \right) = MH\\\left( {MENH} \right) \cap \left( {BCD} \right) = ME\\\left( {MENH} \right) \cap \left( {ABD} \right) = NH\\\left( {MENH} \right) \cap \left( {ACD} \right) = NE\end{array} \right.\) nên thiết diện cần tìm là hình bình hành \(MENH\)
Để \(MENH\) là hình thoi thì \(MH = ME\)
+ Giả sử \(MC = a\left( {0 < a < 9} \right) \Rightarrow MB = 9 - a\)
Theo định lý Ta-lét ta có \(\dfrac{{ME}}{{BD}} = \dfrac{{MC}}{{BC}} \Leftrightarrow \dfrac{{ME}}{3} = \dfrac{a}{9} \Leftrightarrow ME = \dfrac{a}{3}\)
Theo định lý Ta-lét ta có \(\dfrac{{MH}}{{AC}} = \dfrac{{BM}}{{BC}} \Leftrightarrow \dfrac{{MH}}{6} = \dfrac{{9 - a}}{9} \Leftrightarrow MH = \dfrac{{18 - 2a}}{3}\)
Mà \(ME = MH \Leftrightarrow \dfrac{a}{3} = \dfrac{{18 - 2a}}{3} \Leftrightarrow a = 18 - 2a \Leftrightarrow a = 6\)
Suy ra \({M_0}C = 6;{M_0}B = 3 \Rightarrow {M_0}B.{M_0}C = 6.3 = 18\)
Chọn C
Đáp án cần chọn là: C
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
