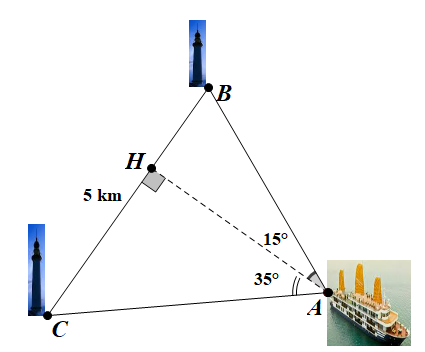
Một người đứng trên tàu thả neo giữa biển phát hiện trên bờ biển có hai ngọn hải đăng
Một người đứng trên tàu thả neo giữa biển phát hiện trên bờ biển có hai ngọn hải đăng cách nhau \(5\,{\rm{km}}\). Người đó xác định được các góc tạo thành giữa các đường ngắm của hai ngọn hải đăng và đường thẳng từ tàu vuông góc với bờ là \({15^0}\)và \({35^0}\)( hình minh họa). Hãy tính khoảng cách giữa con tàu và bờ biển nối hai ngọn hải đăng.
Đáp án đúng là: C
Quảng cáo
- Mô hình hoá bài toán.
- Tính khoảng cách từ tàu đến ngọn hải đăng thứ hai dựa vào định lí sin.
- Tính khoảng cách từ tàu đến bờ biển dựa vào tam giác vuông.
Gọi \(B,\,C\) lần lượt là chân ngọn hải đăng thứ nhất và thứ hai.
Gọi \(A\) là điểm người đứng trên tàu và \(H\) là hình chiếu của \(A\) lên \(BC\).
Trong tam giác\(ABC\)áp dụng định lí sin ta có
\(\dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{BC}}{{\sin \widehat {BAC}}} \Rightarrow AB = \dfrac{{BC.\sin \widehat {ACB}}}{{\sin \widehat {BAC}}} = \dfrac{{5.\sin 55^\circ }}{{\sin 50^\circ }} \approx 5,35\,\,\)(km)
\(\dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {BAC}}} \Rightarrow AC = \dfrac{{BC.\sin \widehat {ABC}}}{{\sin \widehat {BAC}}} = \dfrac{{5.\sin 75^\circ }}{{\sin 50^\circ }} \approx 6,30\,\,\)(km)
Trong tam giác vuông \(AHC\) ta có \(AH = AC.\cos \widehat {HAC} \approx 6,30.\cos 35^\circ \approx 5,16\,\,\)(km).
Đáp án cần chọn là: C
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
