Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Lí 10

Đồ thị vận tốc – thời gian trong hình vẽ là của một xe bus và một xe máy chạy cùng chiều

Đồ thị vận tốc – thời gian trong hình vẽ là của một xe bus và một xe máy chạy cùng chiều trên một đường thẳng. Xe bus đang đứng yên, bắt đầu chuyển động thì xe máy đi tới.

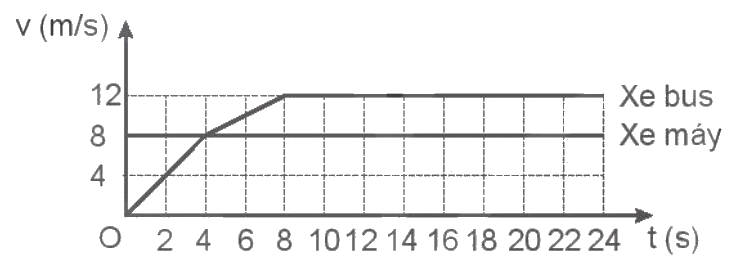
Trả lời cho các câu 1, 2, 3, 4 dưới đây:

Câu hỏi số 1:
Thông hiểu

Khi nào thì xe bus bắt đầu chạy nhanh hơn xe máy?

Đáp án đúng là: A

Xem lời giải
Câu hỏi:588068
Phương pháp giải

Sử dụng kĩ năng đọc đồ thị

Giải chi tiết

Xe bus bắt đầu chạy nhanh hơn xe máy khi vận tốc của hai xe bằng nhau

→ xe bus bắt đầu chạy nhanh hơn xe máy tại thời điểm t = 4 s.

Đáp án cần chọn là: A

Câu hỏi số 2:
Vận dụng

Khi nào thì xe bus đuổi kịp xe máy?

Đáp án đúng là: D

Xem lời giải
Câu hỏi:588069
Phương pháp giải

Phương trình chuyển động thẳng đều: \(x = vt\)

Phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)

Phương trình vận tốc của chuyển động thẳng biến đổi đều: \(v = {v_0} + at\)

Xe bus đuổi kịp xe máy khi: \({x_1} = {x_2}\)

Giải chi tiết

Chọn gốc tọa độ tại vị trí xe bus bắt đầu chuyển động

Gốc thời gian là lúc xe bus bắt đầu chuyển động

Phương trình chuyển động của xe máy là:

\({x_1} = {v_1}t = 8t\,\,\left( m \right)\)

+ Xét chuyển động của xe bus:

- Trong 4 s đầu, xe bus chuyển động nhanh dần đều với gia tốc:

\({a_1} = \dfrac{{{v_1} - {v_0}}}{{{t_1}}} = \dfrac{{8 - 0}}{4} = 2\,\,\left( {m/{s^2}} \right)\)

Phương trình chuyển động của xe bus trong khoảng thời gian này là:

\({x_{21}} = {x_{02}} + {v_{02}}t + \dfrac{1}{2}{a_1}{t^2} = {t^2}\,\,\left( m \right)\)

Xe bus đuổi kịp xe máy trong khoảng thời gian này khi:

\({x_1} = {x_{21}} \Rightarrow 8t = {t^2} \Rightarrow t = 8\,\,\left( s \right) > 4s\,\,\left( {loai} \right)\)

Tại t = 4 s, tọa độ của xe bus là:

\({x_{21}} = {t^2} = {4^2} = 16\,\,\left( m \right)\)

- Trong khoảng thời gian từ 4 s đến 8 s, xe bus chuyển động nhanh dần đều với gia tốc:

\({a_2} = \dfrac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \dfrac{{12 - 8}}{{8 - 4}} = 1\,\,\left( {m/{s^2}} \right)\)

Phương trình chuyển động của xe bus trong khoảng thời gian này là:

\(\begin{array}{l}{x_{22}} = {x_{21}} + {v_1}\left( {t - 4} \right) + \dfrac{1}{2}{a_2}{\left( {t - 4} \right)^2}\\ \Rightarrow {x_{22}} = 16 + 8\left( {t - 4} \right) + 0,5{\left( {t - 4} \right)^2}\,\,\left( m \right)\end{array}\)

Xe bus đuổi kịp xe máy trong khoảng thời gian này khi:

\(\begin{array}{l}{x_1} = {x_{22}} \Rightarrow 8t = 16 + 8.\left( {t - 4} \right) + 0,5.{\left( {t - 4} \right)^2}\\ \Rightarrow 0,5{t^2} - 4t - 8 = 0\\ \Rightarrow t = 9,66\,\,\left( s \right) > 8s\,\,\left( {loai} \right)\end{array}\)

Tại thời điểm 8 s, tọa độ của xe bus là:

\({x_{22}} = 16 + 8.\left( {8 - 4} \right) + 0,5.{\left( {8 - 4} \right)^2} = 56\,\,\left( m \right)\)

- Sau thời điểm 8s, xe bus chuyển động đều với vận tốc: \({v_2} = 12\,\,\left( {m/s} \right)\)

Phương trình chuyển động của xe bus là:

\({x_{23}} = {x_{22}} + {v_2}\left( {t - 8} \right) = 56 + 12\left( {t - 8} \right)\,\,\left( m \right)\)

Xe bus đuổi kịp xe máy khi:

\(\begin{array}{l}{x_1} = {x_{23}} \Rightarrow 8t = 56 + 12.\left( {t - 8} \right)\\ \Rightarrow 4t = 40 \Rightarrow t = 10\,\,\left( s \right)\,\,\left( {t/m} \right)\end{array}\)

Vậy xe bus đuổi kịp xe máy tại thời điểm 10 s.

Đáp án cần chọn là: D

Câu hỏi số 3:
Vận dụng

Xe máy đi được bao nhiêu mét thì bị xe bus đuổi kịp?

Đáp án đúng là: C

Xem lời giải
Câu hỏi:588070
Phương pháp giải

Xe bus đuổi kịp xe máy khi: \({x_1} = {x_2}\)

Giải chi tiết

Tại thời điểm 10 s, xe bus đuổi kịp xe máy, khi đó xe máy đi được quãng đường là:

\(s = {x_1} = 8t = 8.10 = 80\,\,\left( m \right)\)

Đáp án cần chọn là: C

Câu hỏi số 4:
Vận dụng

Tính vận tốc trung bình của xe bus trong 8 s đầu.

Đáp án đúng là: D

Xem lời giải
Câu hỏi:588071
Phương pháp giải

Vận tốc trung bình: \({v_{tb}} = \dfrac{d}{t}\)

Giải chi tiết

Vận tốc trung bình của xe bus trong 8 s đầu là:

\({v_{tb}} = \dfrac{{{x_{22}} - {x_0}}}{t} = \dfrac{{56}}{8} = 7\,\,\left( {m/s} \right)\)

Đáp án cần chọn là: D

Quảng cáo

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn