Điều tra \(42\) học sinh của một lớp \(11\) về số giờ tự học ở nhà, người ta có bảng sau
Điều tra \(42\) học sinh của một lớp \(11\) về số giờ tự học ở nhà, người ta có bảng sau đây:
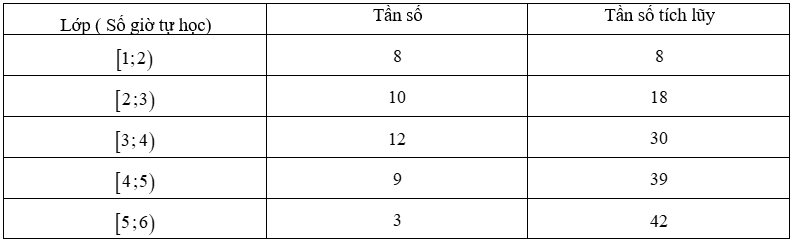
Tứ phân vị thứ nhất của mẫu số liệu trên là.
Đáp án đúng là: A
Quảng cáo
Trung vị \({{\rm{M}}_e}\) là tứ phân vị thứ hai \({{\rm{Q}}_2}\).
Giả sử nhóm \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\dfrac{n}{4}\) tức là \(c{f_{p - 1}} < \dfrac{n}{4}\) nhưng \(c{f_p} \ge \dfrac{n}{4}\). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p;c{f_{p - 1}}\) là tần số tích luỹ của nhóm \(p - 1\).
Tứ phân vị thứ nhất, \({Q_1}\) được tính bằng công thức sau: \({{\rm{Q}}_1} = s + \left( {\dfrac{{\dfrac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right) \cdot h\)
Trung vị \({{\rm{M}}_e}\) là tứ phân vị thứ hai \({{\rm{Q}}_2}\). Giả sử nhóm \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hớn hoặc bằng \(\dfrac{{3n}}{4}\), tức là \(c{f_{q - 1}} < \dfrac{{3n}}{4}\) nhưng \(c{f_q} \ge \dfrac{{3n}}{4}\). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\); \(c{f_{q - 1}}\) là tần số tích luỹ của nhóm \(q - 1\).
Tứ phân vị thứ ba, \({Q_3}\) được tính bằng công thức sau: \({{\rm{Q}}_3} = t + \left( {\dfrac{{\dfrac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right) \cdot l\)
Đáp án cần chọn là: A
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
