Cho hàm số \(y = \dfrac{{{x^2} + mx + 1}}{{x + m}}\) (tham số \(m\) ). Khi đó:
Cho hàm số \(y = \dfrac{{{x^2} + mx + 1}}{{x + m}}\) (tham số \(m\) ). Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) a) Khi \(m = 1\) hàm số có 2 điểm cực trị |
||
| b) b) Khi \(m = 1\) hàm số đồng biến trên khoảng \((0; + \infty )\) |
||
| c) c) Để hàm số liên tục trên [0 ; 2] thì \(\left[ {\begin{array}{*{20}{l}}{m > 0}\\{m < - 2}\end{array}} \right.\) |
||
| d) d) Để hàm số \(y = \dfrac{{{x^2} + mx + 1}}{{x + m}}\) liên tục và đạt giá trị nhỏ nhất trên đoạn [0 ; 2] tại một điểm \({x_0} \in (0;2)\) thì \(m > 1\). |
Đáp án đúng là: Đ; Đ; Đ; S
Quảng cáo
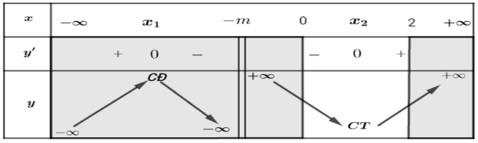
1. Xác định miền xác định $D=\mathbb{R} \backslash\{-m\} \Rightarrow$ yêu cầu liên tục trên $[0,2]$ là $-m \notin[0,2](=>m<-2$ hoặc $m>0)$.
2. Tính đạo hàm $y^{\prime}=\frac{(x+m)^2-1}{(x+m)^2}$, giải $y^{\prime}=0$ để tìm các điểm tới hạn $x=-m \pm 1$.
3. Lập bảng biến thiên (kết hợp với điều kiện xác định) để xác định cực trị / giá trị nhỏ nhất hoặc lớn nhất trên đoạn cần xét.
Tập xác định: \(D = \mathbb{R}\backslash \{ - m\} \). Hàm số liên tục trên \([0;2] \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - m < 0}\\{ - m > 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 0}\\{m < - 2}\end{array}} \right.} \right.\)
Vậy c đúng
Ta có \({y^\prime } = \dfrac{{{x^2} + 2mx + {m^2} - 1}}{{{{(x + m)}^2}}} = \dfrac{{{{(x + m)}^2} - 1}}{{{{(x + m)}^2}}}\).
Cho \({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_1} = - m - 1}\\{{x_2} = - m + 1}\end{array}} \right.\).
Với $m=1$ hàm số có 2 cực trị $x=-2$ và $x=0$ nên a đúng
Với $m=1$ thì hàm số luôn đồng biến trên \((0; + \infty )\) nên b đúng
Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại \({x_0} \in (0;2)\) nên \(0 < - m + 1 < 2 \Leftrightarrow - 1 < m < 1\) So với điều kiện hàm số liên tục trên đoạn [0 ; 2]. Ta có \(0 < m < 1\).
Đáp án cần chọn là: Đ; Đ; Đ; S
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
