Đoạn mạch AB như hình H1 là mạch điện xoay chiều gồm một điện trở R, cuộn cảm thuần L có

Câu hỏi số 710135:

Vận dụng cao

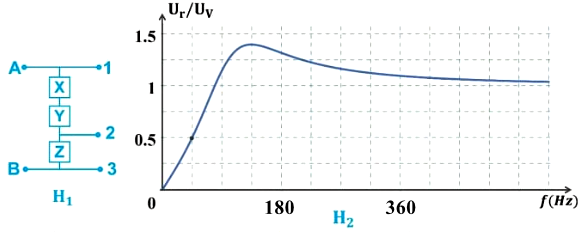
Đoạn mạch AB như hình H1 là mạch điện xoay chiều gồm một điện trở R, cuộn cảm thuần L có độ tự cảm 0,318H và một tụ điện C có điện dung 8,00μF mắc nối tiếp. Các phân tử được mắc trong hộp không rõ thứ tự nên mỗi phần tử X, Y, Z của mạch điện là một trong ba phần tử R, L, C. Mạch được sử dụng như một bộ lọc tín hiệu với nguyên tắc: tín hiệu vào là một điện áp xoay chiều có giá trị hiệu dụng \({U_V}\) và tần số f được đưa vào hai đầu A và B, tín hiệu ra là điện áp giữa hai trong ba đầu ra được đánh số 1, 2 và 3 như hình H1, tín hiệu ra sẽ có cùng tần số f và có giá trị hiệu dụng \({U_r}\); bộ lọc “chặn” tín hiệu khi \({U_r} < 0,5{U_V}\) và cho tín hiệu “qua” khi \({U_r} \ge 0,5{U_V}.\) Hình H2 là đồ thị mô tả sự phụ thuộc của tỉ số \(\dfrac{{{U_r}}}{{{U_v}}}\) theo tần số f khi hai đầu ra là 1 và 2. Lấy \(\pi \approx 3,14.\) Nếu chọn hai đầu ra là 2 và 3 thì bộ lọc này cho tín hiệu “qua” khi tín hiệu có tần số f nằm trong khoảng

A. từ 0 đến 156 Hz.

B. từ 982 Hz trở lên.

C. từ 156 Hz đến 313 Hz.

D. từ 313 Hz đến 982 Hz.

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:710135

Phương pháp giải

Xác định tần số của mạch để xảy ra cộng hưởng.

Xác định các phần tử thuộc các hộp X, Y và Z.

Với \({f_1} = 45\left( {Hz} \right)\), tính cảm kháng, dung kháng và điện trở R.

Biện luận theo bộ lọc “chặn” tín hiệu khi \({U_r} < 0,5{U_V}\) và cho tín hiệu “qua” khi \({U_r} \ge 0,5{U_V}.\)

Giải chi tiết

Tần số của mạch lúc cộng hưởng:

\({f_0} = \dfrac{1}{{2\pi \sqrt {LC} }} \approx 99,83\left( {Hz} \right)\)

Nếu hộp Z không chứa tụ điện thì \(f = 0\) ta có \({Z_C} \to \infty \)

\( \Rightarrow I = 0 \Rightarrow {U_Z} = 0 \Rightarrow {U_{12}} = U.\) Mâu thuẫn với đồ thị đã cho. Vậy hộp Z chứa tụ điện.

Do đó, ta có: \({U_{12}} = \dfrac{U}{{\sqrt {1 + \dfrac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}\)

Ứng với \({f_1} = 45\left( {Hz} \right)\) ta có: \({Z_L} = 90\Omega ;{\rm{ }}{Z_C} = 442,32\Omega .\)

Theo đồ thị, lúc này:

\(\begin{array}{l}{U_{12}} = 0,5U \Rightarrow 1 + \dfrac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}} = 4\\ \Rightarrow R \approx 174,86\Omega \Rightarrow \alpha = \dfrac{{{R^2}}}{{2{Z_L}{Z_C}}} \approx 0,384\end{array}\)

Ta có: \(U_C^2 = \dfrac{{{U^2}Z_C^2}}{{{Z^2}}} = \dfrac{{{U^2}}}{{{x^2} - 2\left( {1 - \alpha } \right).x + 1}}\) với \(x = \dfrac{{{\omega ^2}}}{{\omega _0^2}} = \dfrac{{{f^2}}}{{f_0^2}}\)

Để bộ lọc ứng với hai đầu 2 – 3 cho tín hiệu qua ta phải có:

\(\begin{array}{l}\dfrac{{U_C^2}}{{{U^2}}} = \dfrac{1}{{{x^2} - 2\left( {1 - \alpha } \right).x + 1}} \ge \dfrac{1}{4}\\ \Rightarrow {x^2} - 2\left( {1 - \alpha } \right).x - 3 \le 0\\ \Rightarrow {x^2} - 1,232x - 3 \le 0\end{array}\)

Giải bất phương trình trên và loại nghiệm âm ta được: \(0 \le x \le 2,45\)

\( \Rightarrow 0 \le f \le {f_0}\sqrt {2,45} \approx 156,3\left( {Hz} \right)\)

Đáp án cần chọn là: A

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.