Trong một cuộc thi về “bữa ăn dinh dưỡng”, ban tổ chức yêu cầu để đảm bảo
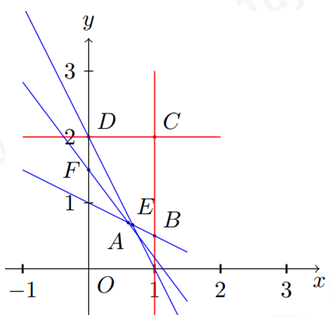
Trong một cuộc thi về “bữa ăn dinh dưỡng”, ban tổ chức yêu cầu để đảm bảo lượng dinh dưỡng hằng ngày thì mỗi gia đình có \(4\) thành viên cần ít nhất \(900\) đơn vị prôtêin và \(400\) đơn vị lipít trong thức ăn hằng ngày. Mỗi kg thịt bò chứa \(800\) đơn vị prôtêin và \(200\) đơn vị lipit, \(1{\rm{ (kg)}}\) thịt heo chứa \(600\) đơn vị prôtêin và \(400\)đơn vị lipit. Biết rằng người nội trợ chỉ được chi tối đa \(200\) ngàn đồng để mua thịt. Biết rằng \(1{\rm{ (kg)}}\) thịt bò giá \(200\) ngàn đồng, \(1{\rm{ (kg)}}\) thịt heo giá \(100\) ngàn đồng. Người nội trợ nên mua \(x{\rm{ (kg)}}\) thịt bò và \(y{\rm{ (kg)}}\) thịt heo để phí thấp nhất cho khẩu phần thức ăn mà vẫn đảm bảo chất dinh dưỡng, khi đó hãy tìm \(x + 2y.\)
Đáp án đúng là:
Quảng cáo
Từ giả thiết ta suy ra \(0 \le x \le 1,\,\,0 \le y \le 2\)
Chi phí để mua thức ăn là \(f\left( {x;y} \right) = 200000x + 100000y\)
Lượng protein cung cấp là \(g\left( {x;y} \right) = 800x + 600y\)
Lượng lipid cung cấp là \(h\left( {x;y} \right) = 200x + 400y\)
Theo giả thiết \(\left\{ \begin{array}{l}800x + 600y \ge 900\\200x + 400y \ge 400\\200000x + 100000y \le 200000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x + 6y \ge 9\\x + 2y \ge 2\\2x + y \le 2\end{array} \right.\)
Ta có hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 1\\0 \le y \le 2\\8x + 6y \ge 9\\x + 2y \ge 2\\2x + y \le 2\end{array} \right.\)
Miền nghiệm của hệ bất phương trình là tứ giác AEDF với \(A\left( {\dfrac{2}{3};\dfrac{2}{3}} \right)\), \(E\left( {0,6;0,7} \right)\), \(D\left( {0;2} \right)\), \(F\left( {0;\dfrac{3}{2}} \right)\)
Xét tại biên A, D, E, F có
\(\begin{array}{l}A\left( {\dfrac{2}{3};\dfrac{2}{3}} \right),\,\,f\left( {\dfrac{2}{3};\dfrac{2}{3}} \right) = 200000\\D\left( {0;2} \right),\,\,f\left( {0;2} \right) = 200000\\E\left( {0,6;0,7} \right),\,\,f\left( {0,6;0,7} \right) = 190000\\F\left( {0;\dfrac{3}{2}} \right),\,\,f\left( {0;\dfrac{3}{2}} \right) = 150000\end{array}\)
Vậy chi phí thấp nhất là 150000 đồng với \(x = 0,\,\,y = \dfrac{3}{2} \Rightarrow x + 2y = 3\)
Đáp án cần điền là: 3
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
