Trong một nhà máy sản xuất, có hai bánh răng tròn lớn và nhỏ

Câu hỏi số 742890:

Vận dụng

Trong một nhà máy sản xuất, có hai bánh răng tròn lớn và nhỏ được đặt trong một cơ cấu máy móc.

- Bánh răng lớn có tâm $O_1$, bán kính 10 cm .

- Bánh răng nhỏ có tâm $O_2$ với bán kính 6 cm .

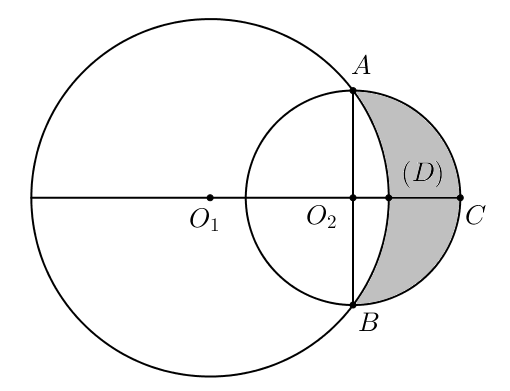
Hai bánh răng này cắt nhau tại hai điểm A và B, với đoạn thẳng AB là đường kính của bánh răng nhỏ. Để đảm bảo vận hành trơn tru, người kỹ sư cần thiết kế một phần đệm bôi trơn nằm ngoài phần giao của hai bánh răng. Phần đệm này sẽ được tạo thành bằng cách quay vùng không giao của bánh răng nhỏ với bánh răng lớn (phần gạch chéo trong hình vẽ) quanh đường thẳng nối tâm hai bánh răng ${{O}_{1}}{{O}_{2}}$. Hãy tính thể tích V của phần đệm này để xác định lượng vật liệu cần chế tạo. (Làm tròn kết quả đến hàng đơn vị).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:742890

Phương pháp giải

Viết phương trình hai đường tròn và đưa về tính thể tích bằng tích phân

Giải chi tiết

Chọn hệ tọa độ Oxy với ${{\rm{O}}_2} \equiv {\rm{O}},{{\rm{O}}_2}{\rm{C}} \equiv {\rm{Ox}},{{\rm{O}}_2}{\rm{\;A}} \equiv {\rm{Oy}}$.

Cạnh ${O_1}{O_2} = \sqrt {{O_1}{A^2} - {O_2}{A^2}} = \sqrt {{{10}^2} - {6^2}} = 8 \Rightarrow \left( {{O_1}} \right):{(x + 8)^2} + {y^2} = 100$.

Phương trình đường tròn $\left( {{O_2}} \right):{x^2} + {y^2} = 36$.

Kí hiệu $\left( {{H_1}} \right)$ là hình phẳng giới hạn bởi các đường $y = \sqrt {100 - {{(x + 8)}^2}}$, trục $Ox,x = 0$, $x = 2$.

Kí hiệu $\left( {{{\rm{H}}_2}} \right)$ là hình phẳng giới hạn bởi các đường $y = \sqrt {36 - {x^2}}$, trục $Ox,x = 0,x = 6$.

Khi đó thể tích $V$ cần tính chính bằng thể tích ${V_2}$ của khối tròn xoay thu được khi quay hình $\left( {{{\rm{H}}_2}} \right)$ xung quanh trục Ox trừ đi thể tích ${V_1}$ của khối tròn xoay thu được khi quay hình $\left( {{H_1}} \right)$ xung quanh trục Ox.

Ta có ${V_2} = \dfrac{1}{2} \cdot \dfrac{4}{3}\pi {r^3} = \dfrac{2}{3}\pi \cdot {6^3} = 144\pi$.

Lại có ${{V}_{1}}=\pi \int\limits_{0}^{2}{{{\left( \sqrt{100-{{\left( x+8 \right)}^{2}}} \right)}^{2}}dx}=\dfrac{112}{3}\pi $

Do đó $V={{V}_{2}}-{{V}_{1}}=144\pi \text{ }\!\!~\!\!\text{ }-\dfrac{112\pi }{3}=\dfrac{320\pi }{3}\approx 335$.

Đáp án cần điền là: 335

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.