Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Hình vẽ mô tả một ngôi nhà một tầng đơn giản đặt trên một mặt

Câu hỏi số 746849:
Vận dụng

Hình vẽ mô tả một ngôi nhà một tầng đơn giản đặt trên một mặt phẳng nằm ngang.

Trên một trong hai mặt mái hình chữ nhật, người ta muốn xây dựng một cửa sổ mái.

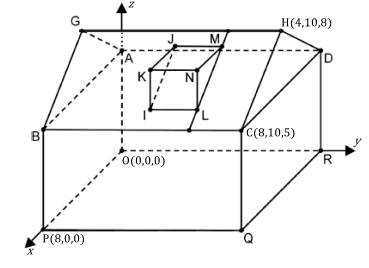
Các điểm A, B, C, D, O, P, Q và R là các đỉnh của một hình hộp chữ nhật. Hình lăng trụ đứng tam giác LMNIJK biểu diễn cửa sổ mái, đoạn thẳng GH là đỉnh mái. Một đơn vị độ dài trong hệ tọa độ tương ứng với 1m, nghĩa là ngôi nhà dài 10m.

Đúng Sai
a) Theo quy định xây dựng của thành phố, để được phép xây dựng cửa sổ mái, góc nghiêng của mặt mái so với phương ngang phải ít nhất là \(35^0\). Góc nghiêng của mặt mái nhà ở trên với phương ngang bằng \(106,{26^0}\) nên đã đáp ứng yêu cầu để xây dựng cửa sổ mái.
b) Phương trình mặt phẳng mái nhà để xây dựng cửa sổ có dạng \(ax + by + cz + d = 0\) với \(a + b + c + d = - 37\).
c) Biết đường thẳng LM cắt đỉnh mái GH tại \(T\left( {4,8,8} \right)\) và M cách đỉnh mái GH là 1m. Tọa độ của \(M\left( {m,n,p} \right)\) thỏa mãn \(25mnp = 7014\)
d) Phương trình mặt phẳng MNKJ là \(z = \dfrac{{37}}{5}\)

Đáp án đúng là: S; Đ; S; Đ

Quảng cáo

Xem lời giải
Câu hỏi:746849
Phương pháp giải

Dựa vào tọa độ các đỉnh đã biết trên hình vẽ và tính chất của hình hộp, hình lăng trụ xác định tọa độ của các đỉnh còn lại. Từ đó viết phương trình đường thẳng, mặt phẳng, tọa độ điểm bài yêu cầu.

Giải chi tiết

a) Sai. Do ABCDOPQR là hình hộp chữ nhật với các trục như hình vẽ nên ta có tọa độ các điểm

\(Q\left( {8,10,0} \right),R\left( {0,10,0} \right),B\left( {8,0,5} \right),A\left( {0,0,5} \right),D\left( {0,10,5} \right),G\left( {4,0,8} \right)\)

Khi đó góc giữa mặt phẳng mái nhà với phương ngang chính là \(\angle HCD\)

Từ tọa độ các đỉnh ta có \(\overrightarrow {HC} \left( {4,0, - 3} \right) \Rightarrow HC = 5;\overrightarrow {HD} \left( { - 4,0, - 3} \right) \Rightarrow HD = 5;CD = OP = 8\)

\( \Rightarrow \cos HCD = \dfrac{{C{H^2} + C{D^2} - H{C^2}}}{{2CH.CD}} = \dfrac{{{5^2} + {8^2} - {5^2}}}{{2.5.8}} = \dfrac{4}{5} \Rightarrow \angle HCD = 36,{86^0} > {35^0}\)

Vậy căn nhà đạt tiêu chuẩn xây cửa sổ.

b) Đúng. Phương trình mặt phẳng mái nhà để xât dựng cửa sổ là \(\left( {HCBG} \right)\)

Ta có \(\overrightarrow {HC} \left( {4,0, - 3} \right),\overrightarrow {CB} \left( {0, - 10,0} \right)\)

\(\left( {HCBG} \right)\) có VTPT là \(\overrightarrow n \) thỏa mãn \(\overrightarrow n  \bot \overrightarrow {HC} ,\overrightarrow n  \bot \overrightarrow {CB} \)

\( \Rightarrow \overrightarrow n  = \left[ {\overrightarrow {HC} ,\overrightarrow {CB} } \right] = \left( { - 30,0, - 40} \right) =  - 10\left( {3,0,4} \right)\)

Khi đó \(\left( {HCBG} \right)\) qua \(B\left( {8,0,5} \right),\)vtpt \(\overrightarrow n \left( {3,0,4} \right)\) là:

\(3\left( {x - 8} \right) + 4\left( {y - 5} \right) = 0 \Leftrightarrow 3x + 4y - 44 = 0\)

c) Sai. LM qua \(T\left( {4,8,8} \right)\) và song song với HC nên nhận \(\overrightarrow {HC} \left( {4,0, - 3} \right)\) là VTCP

Khi đó phương trình tham số của LM là \(\left\{ \begin{array}{l}x = 4 + 4t\\y = 8\\z = 8 - 3t\end{array} \right.\)

Gọi \(M \in LM \Rightarrow M\left( {4 + 4t,8,8 - 3t} \right)\)

Do M cách đỉnh mái HG bằng 1m nên \(MT = 1\)

\( \Rightarrow {\left( {4 + 4t - 4} \right)^2} + {0^2} + {\left( {8 - 3t - 8} \right)^2} = 1 \Leftrightarrow t =  \pm \dfrac{1}{5}\)

Do M cách mặt đất thấp hơn T nên \(t = \dfrac{1}{5} \Rightarrow M\left( {\dfrac{{24}}{5},8,\dfrac{{37}}{5}} \right) \Rightarrow 25mnp = 7104\)

d) Đúng. Ta có (MNKJ) là mặt phẳng song song với đáy nên có dạng \(z = a\).

Do (MNKJ) chứa \(M\left( {\dfrac{{24}}{5},8,\dfrac{{37}}{5}} \right)\) cách đáy bằng \(\dfrac{{37}}{5} \Rightarrow \)\(\left( {MNKJ} \right):z = \dfrac{{37}}{5}\).

Đáp án cần chọn là: S; Đ; S; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn