Trên một sân chơi, người ta dựng một tấm vải buồm hình tam giác để che
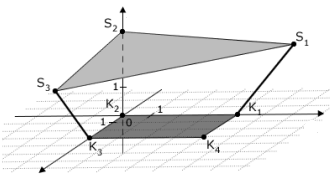
Trên một sân chơi, người ta dựng một tấm vải buồm hình tam giác để che bóng cho một cái bể cát. Để làm điều này, người ta gắn các thanh kim loại vào ba góc của bể cát và cố định tấm vải buồm vào các đầu của thanh. Trong hệ trục tọa độ, mặt phẳng Oxy biểu diễn mặt đất nằm ngang. Bể cát được mô tả bởi hình chữ nhật có các đỉnh \({K_1}(0;4;0)\),\({K_2}(0;0;0)\), \({K_3}(3;0;0)\) và \({K_4}(3;4;0)\). Tấm vải buồm được mô tả bởi tam giác có các đỉnh \({S_1}\left( {0;6;\dfrac{5}{2}} \right)\), \({S_2}(0;0;3)\) và \({S_3}\left( {6;0;\dfrac{5}{2}} \right)\). Một đơn vị độ dài trong hệ tọa độ tương ứng với một mét trong thực tế. (Nguồn: abiturloesung.de)
| Đúng | Sai | |
|---|---|---|
| a) Mặt phẳng chứa tấm vải có phương trình: \(x + y + 12z - 36 = 0\). | ||
| b) Nhà sản xuất tấm vải buồm khuyến cáo nên sử dụng thêm dây cáp để cố định các thanh kim loại khi diện tích tấm vải buồm lớn hơn \(20\;{{\rm{m}}^2}\). Trong trường hợp này, không cần thiết phải sử dụng dây cáp. | ||
| c) Để đảm bảo nước mưa có thể thoát đi, tấm vải buồm phải có góc nghiêng so với mặt đất ít nhất \({8^\circ }\). Trong trường hợp này, nước mưa không thể thoát đi. | ||
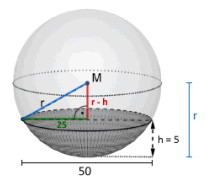
| d) Khi trời mưa lớn, tấm vải buồm bị biến dạng và trũng xuống, tạo thành một "túi nước" chứa nước mưa không thể thoát ra được. Chỗ trũng có miệng hình tròn với đường kính 50 cm và ở điểm sâu nhất, túi nước sâu 5 cm. Để đơn giản, ta coi túi nước này là một phần của hình cầu. Thể tích V của một phần hình cầu có thể tính bằng công thức \(V = \dfrac{1}{3}\pi {h^2} \cdot (3r - h)\), trong đó \(r\) là bán kính của hình cầu và \(h\) là chiều cao. Túi nước này chứa được \(5000\;{\rm{c}}{{\rm{m}}^3}\) nước (kết quả làm tròn đến hàng đơn vị).
|
Đáp án đúng là: Đ; Đ; Đ; S
Quảng cáo
a) Viết phương trình mặt phẳng đi qua \(S_1\) và có cặp vectơ chỉ phương \(\overrightarrow {S_2S_1}\), \(\overrightarrow {S_2S_3}\).
b) Sử dụng công thức: \(S = \dfrac{1}{2}\left| {\left[ {\overrightarrow {{S_2}{S_1}} ,\overrightarrow {{S_2}{S_3}} } \right]} \right|\).
c) Sử dụng công thức tính góc: \(\cos \left( {\overrightarrow n ,\overrightarrow m } \right) = \dfrac{{\overrightarrow n .\overrightarrow m }}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow m } \right|}}\).
d) Có \(h=5\), sử dụng định lí pythagoras giải phương trình tính bán kính \(r\), thay vào công thức tính thể tích.
a) Đúng: Có \({S_1}\left( {0;6;\dfrac{5}{2}} \right)\), \({S_2}(0;0;3)\) và \({S_3}\left( {6;0;\dfrac{5}{2}} \right)\)
\(\overrightarrow {{S_2}{S_1}} \left( {0;6; - \dfrac{1}{2}} \right)\); \(\overrightarrow {{S_2}{S_3}} \left( {6;0; - \dfrac{1}{2}} \right)\).
Suy ra \(\left[ {\overrightarrow {{S_2}{S_1}} ,\overrightarrow {{S_2}{S_3}} } \right] = \left( {3;3;36} \right).\)
Mặt phẳng chứa tấm vải đi qua \({S_1}\left( {0;6;\dfrac{5}{2}} \right)\) và nhận \(\overrightarrow n = \dfrac{1}{3}\left[ {\overrightarrow {{S_2}{S_1}} ,\overrightarrow {{S_2}{S_3}} } \right] = \left( {1;1;12} \right)\) làm vectơ pháp tuyến.
Mặt phẳng chứa tấm vải có phương trình: \(x + y + 12z - 36 = 0\).
b) Đúng: Diện tích tấm vải là:
\(S = \dfrac{1}{2}\left| {\left[ {\overrightarrow {{S_2}{S_1}} ,\overrightarrow {{S_2}{S_3}} } \right]} \right| = \dfrac{1}{2}\left| {\left( {3;3;36} \right)} \right| = \dfrac{1}{2}\sqrt {{3^2} + {3^2} + {{36}^2}} \approx 18,12.\)
Vậy trong trường hợp này, không cần thiết phải sử dụng dây cáp.
c) Đúng: Mặt đất là mặt phẳng \(Oxy\) có vectơ pháp tuyến là \(\overrightarrow m (0;0;1)\).
Có \(\overrightarrow n \left( {1;1;12} \right)\), suy ra \(\overrightarrow n .\overrightarrow m = 1.0 + 1.0 + 12.1 = 12.\)
\(\left| {\overrightarrow n } \right| = \sqrt {{1^2} + {1^2} + {{12}^2}} = \sqrt {146} \); \(\left| {\overrightarrow m } \right| = 1.\)
Góc giữa tấm vải và mặt đất là
\(\cos \left( {\overrightarrow n ,\overrightarrow m } \right) = \dfrac{{\overrightarrow n .\overrightarrow m }}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow m } \right|}} = \dfrac{{12}}{{\sqrt {146} }} \Rightarrow \left( {\overrightarrow n ,\overrightarrow m } \right) \approx 6,{7^o} < {8^o}.\)
Vậy trong trường hợp này, nước mưa không thể thoát đi.
d) Sai:
Ta có \({25^2} + {(r - 5)^2} = {r^2}\)
\( \Leftrightarrow 625 + {r^2} - 10r + 25 = {r^2}\)
\( \Leftrightarrow 650 - 10r = 0\)
\( \Leftrightarrow r = 65\;{\rm{cm}}\)
Thể tích phần hình cầu là: \(V = \dfrac{1}{3}\pi \cdot {5^2} \cdot (3 \cdot 65 - 5) \approx 4974\;{\rm{c}}{{\rm{m}}^3}\)
Vậy túi nước này chứa được khoảng \({\rm{4974c}}{{\rm{m}}^3}\) nước.
Đáp án cần chọn là: Đ; Đ; Đ; S
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
