Một chiếc điện thoại iphone được đặt trên một giá đỡ có ba chân với

Câu hỏi số 749986:

Vận dụng

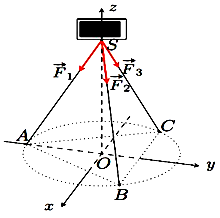
Một chiếc điện thoại iphone được đặt trên một giá đỡ có ba chân với điểm đặt \(S\left( {0;0;20} \right)\) và các điểm chạm mặt đất của ba chân lần lượt là \(A\left( {0; - 6;0} \right),B\left( {3\sqrt 3 ;3;0} \right),C\left( { - 3\sqrt 3 ;3;0} \right)\) (đơn vị cm ). Cho biết điện thoại có trọng lượng là 2 N và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực \({\vec F_1},{\vec F_2},{\vec F_3}\) có độ lớn bằng nhau. Biết tọa độ của lực \(\overrightarrow {{F_1}} = \left( {a;b;c} \right)\), khi đó \(T = 2a + 5b + 6c\) bằng?

Đáp án:

Đáp án đúng là: -5

Quảng cáo

Xem lời giải

Câu hỏi:749986

Phương pháp giải

Vì chiếc máy cân bằng nên trọng lực của máy sẽ phân bố đều trên các chân của giá đỡ. Từ tọa độ các điểm đã cho, ta tìm được cái mối liên hệ với vecto lực và tìm được tọa độ của các vecto lực.

Tổng hợp lực \(\overrightarrow P + \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)

Giải chi tiết

\(\begin{array}{l}\overrightarrow {SA} \left( {0, - 6, - 20} \right),\overrightarrow {SB} \left( {3\sqrt 3 ,3, - 20} \right),\overrightarrow {SC} \left( { - 3\sqrt 3 ,3, - 20} \right)\\ \Rightarrow \left\{ \begin{array}{l}SA = SB = SC = 2\sqrt {109} \\\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \left( {0,0, - 60} \right)\end{array} \right.\end{array}\)

Do các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng phương với các giá đỡ và có độ lớn bằng nhau nên

\(\dfrac{{\left| {\overrightarrow {{F_1}} } \right|}}{{SA}} = \dfrac{{\left| {\overrightarrow {{F_2}} } \right|}}{{SB}} = \dfrac{{\left| {\overrightarrow {{F_3}} } \right|}}{{SC}} = k \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{F_1}} = k\overrightarrow {SA} \\\overrightarrow {{F_2}} = k\overrightarrow {SB} \\\overrightarrow {{F_3}} = k\overrightarrow {SC} \end{array} \right. \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = k\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) = k\left( {0,0, - 20} \right)\)

\( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \left( {0,0, - 60k} \right)\)

\( \Rightarrow P = 60k = 2 \Rightarrow k = \dfrac{1}{{30}} \Rightarrow \overrightarrow {{F_1}} = \left( {0, - \dfrac{1}{5}, - \dfrac{2}{3}} \right) \Rightarrow 2a + 5b + 6c = - 5\)

Đáp án cần điền là: -5

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.